Sequence to General Tree: Knowledge-Guided Geometry Word Problem Solving

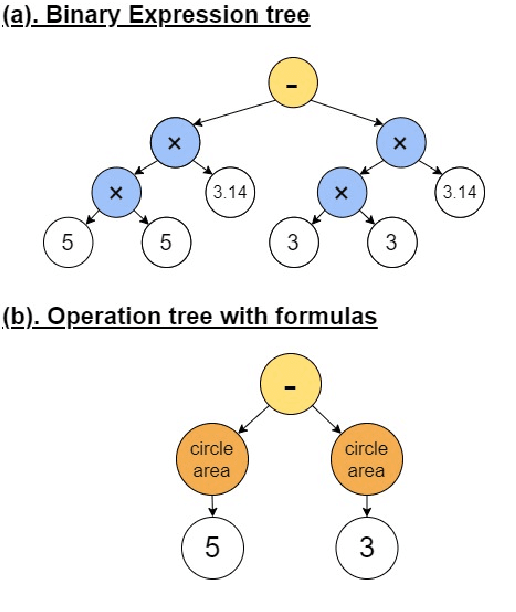
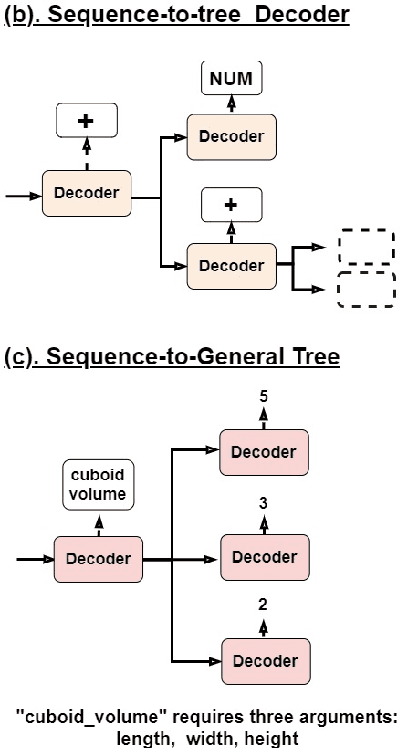
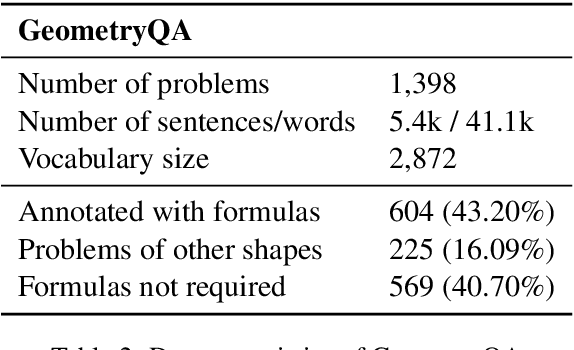
With the recent advancements in deep learning, neural solvers have gained promising results in solving math word problems. However, these SOTA solvers only generate binary expression trees that contain basic arithmetic operators and do not explicitly use the math formulas. As a result, the expression trees they produce are lengthy and uninterpretable because they need to use multiple operators and constants to represent one single formula. In this paper, we propose sequence-to-general tree (S2G) that learns to generate interpretable and executable operation trees where the nodes can be formulas with an arbitrary number of arguments. With nodes now allowed to be formulas, S2G can learn to incorporate mathematical domain knowledge into problem-solving, making the results more interpretable. Experiments show that S2G can achieve a better performance against strong baselines on problems that require domain knowledge.