Error-mitigated Quantum Approximate Optimization via Learning-based Adaptive Optimization

Combinatorial optimization problems are ubiquitous and computationally hard to solve in general. Quantum computing is envisioned as a powerful tool offering potential computational advantages for solving some of these problems. Quantum approximate optimization algorithm (QAOA), one of the most representative quantum-classical hybrid algorithms, is designed to solve certain combinatorial optimization problems by transforming a discrete optimization problem into a classical optimization problem over a continuous circuit parameter domain. QAOA objective landscape over the parameter variables is notorious for pervasive local minima and barren plateaus, and its viability in training significantly relies on the efficacy of the classical optimization algorithm. To enhance the performance of QAOA, we design double adaptive-region Bayesian optimization (DARBO), an adaptive classical optimizer for QAOA. Our experimental results demonstrate that the algorithm greatly outperforms conventional gradient-based and gradient-free optimizers in terms of speed, accuracy, and stability. We also address the issues of measurement efficiency and the suppression of quantum noise by successfully conducting the full optimization loop on the superconducting quantum processor. This work helps to unlock the full power of QAOA and paves the way toward achieving quantum advantage in practical classical tasks.

Automatic Differentiable Monte Carlo: Theory and Application

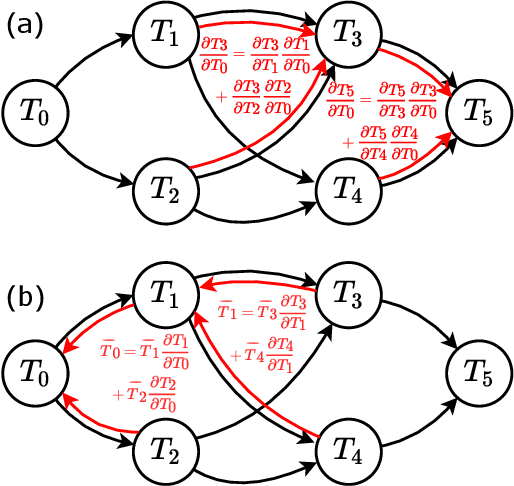
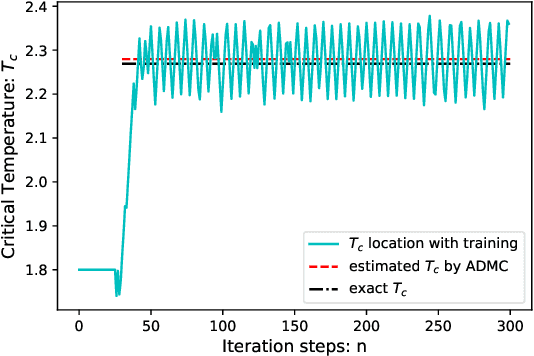
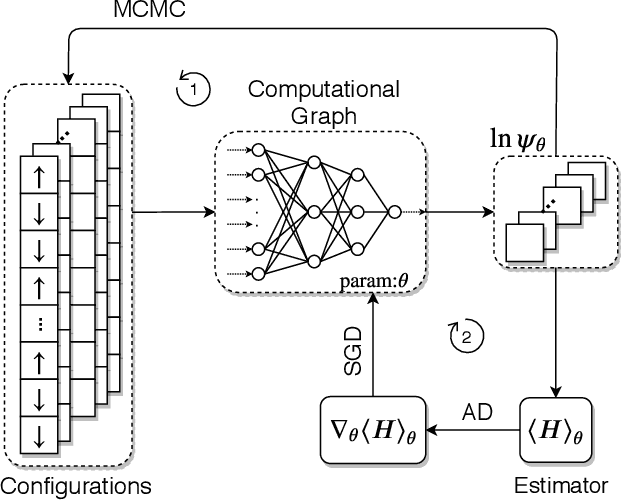
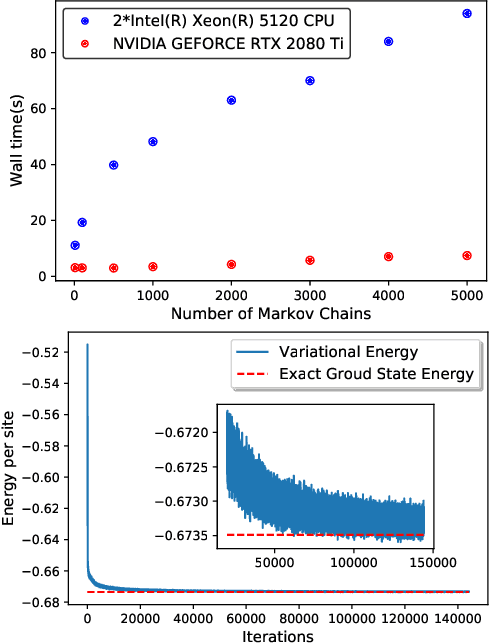
Differentiable programming has emerged as a key programming paradigm empowering rapid developments of deep learning while its applications to important computational methods such as Monte Carlo remain largely unexplored. Here we present the general theory enabling infinite-order automatic differentiation on expectations computed by Monte Carlo with unnormalized probability distributions, which we call "automatic differentiable Monte Carlo" (ADMC). By implementing ADMC algorithms on computational graphs, one can also leverage state-of-the-art machine learning frameworks and techniques to traditional Monte Carlo applications in statistics and physics. We illustrate the versatility of ADMC by showing some applications: fast search of phase transitions and accurately finding ground states of interacting many-body models in two dimensions. ADMC paves a promising way to innovate Monte Carlo in various aspects to achieve higher accuracy and efficiency, e.g. easing or solving the sign problem of quantum many-body models through ADMC.

Automatic Differentiation for Complex Valued SVD

In this note, we report the back propagation formula for complex valued singular value decompositions (SVD). This formula is an important ingredient for a complete automatic differentiation(AD) infrastructure in terms of complex numbers, and it is also the key to understand and utilize AD in tensor networks.