Enhancing High-dimensional Bayesian Optimization by Optimizing the Acquisition Function Maximizer Initialization

Bayesian optimization (BO) is widely used to optimize black-box functions. It works by first building a surrogate for the objective and quantifying the uncertainty in that surrogate. It then decides where to sample by maximizing an acquisition function defined by the surrogate model. Prior approaches typically use randomly generated raw samples to initialize the acquisition function maximizer. However, this strategy is ill-suited for high-dimensional BO. Given the large regions of high posterior uncertainty in high dimensions, a randomly initialized acquisition function maximizer is likely to focus on areas with high posterior uncertainty, leading to overly exploring areas that offer little gain. This paper provides the first comprehensive empirical study to reveal the importance of the initialization phase of acquisition function maximization. It proposes a better initialization approach by employing multiple heuristic optimizers to leverage the knowledge of already evaluated samples to generate initial points to be explored by an acquisition function maximizer. We evaluate our approach on widely used synthetic test functions and real-world applications. Experimental results show that our techniques, while simple, can significantly enhance the standard BO and outperforms state-of-the-art high-dimensional BO techniques by a large margin in most test cases.

Optimizing Sparse Matrix Multiplications for Graph Neural Networks

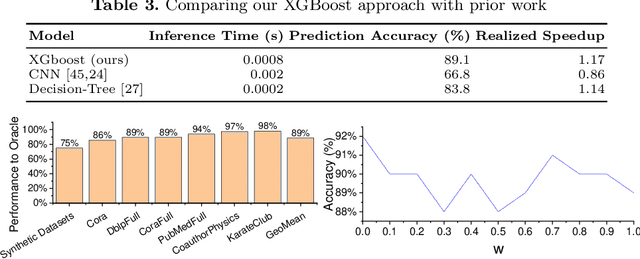
Graph neural networks (GNNs) are emerging as a powerful technique for modeling graph structures. Due to the sparsity of real-world graph data, GNN performance is limited by extensive sparse matrix multiplication (SpMM) operations involved in computation. While the right sparse matrix storage format varies across input data, existing deep learning frameworks employ a single, static storage format, leaving much room for improvement. This paper investigates how the choice of sparse matrix storage formats affect the GNN performance. We observe that choosing a suitable sparse matrix storage format can significantly improve the GNN training performance, but the right format depends on the input workloads and can change as the GNN iterates over the input graph. We then develop a predictive model to dynamically choose a sparse matrix storage format to be used by a GNN layer based on the input matrices. Our model is first trained offline using training matrix samples, and the trained model can be applied to any input matrix and GNN kernels with SpMM computation. We implement our approach on top of PyTorch and apply it to 5 representative GNN models running on a multi-core CPU using real-life and synthetic datasets. Experimental results show that our approach gives an average speedup of 1.17x (up to 3x) for GNN running time.