BDA-PCH: Block-Diagonal Approximation of Positive-Curvature Hessian for Training Neural Networks

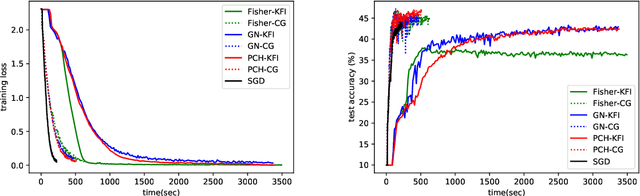
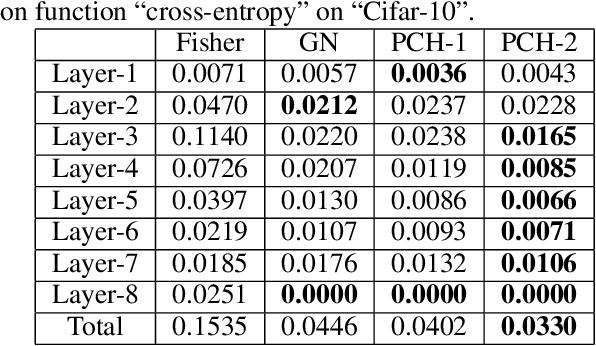
We propose a block-diagonal approximation of the positive-curvature Hessian (BDA-PCH) matrix to measure curvature. Our proposed BDAPCH matrix is memory efficient and can be applied to any fully-connected neural networks where the activation and criterion functions are twice differentiable. Particularly, our BDA-PCH matrix can handle non-convex criterion functions. We devise an efficient scheme utilizing the conjugate gradient method to derive Newton directions for mini-batch setting. Empirical studies show that our method outperforms the competing second-order methods in convergence speed.