Automatic Differentiation of Optimization Algorithms with Time-Varying Updates

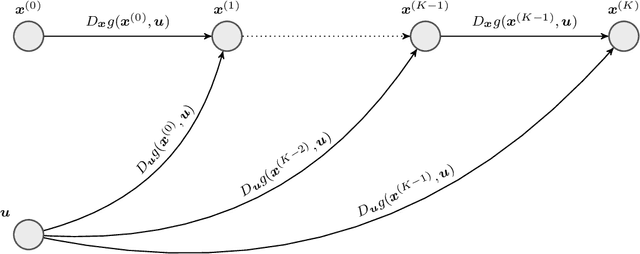
Numerous Optimization Algorithms have a time-varying update rule thanks to, for instance, a changing step size, momentum parameter or, Hessian approximation. In this paper, we apply unrolled or automatic differentiation to a time-varying iterative process and provide convergence (rate) guarantees for the resulting derivative iterates. We adapt these convergence results and apply them to proximal gradient descent with variable step size and FISTA when solving partly smooth problems. We confirm our findings numerically by solving $\ell_1$ and $\ell_2$-regularized linear and logisitc regression respectively. Our theoretical and numerical results show that the convergence rate of the algorithm is reflected in its derivative iterates.

Fixed-Point Automatic Differentiation of Forward--Backward Splitting Algorithms for Partly Smooth Functions

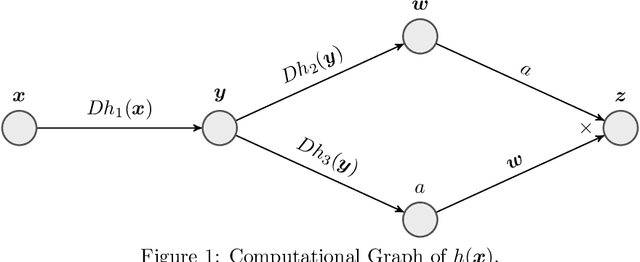
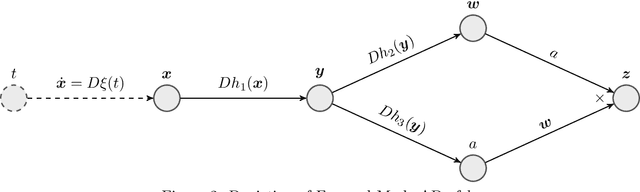
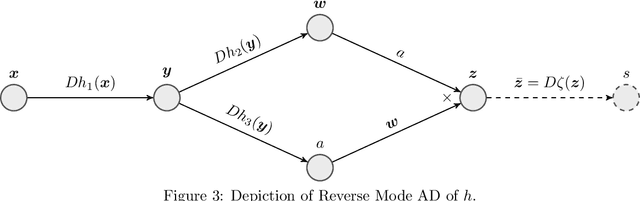
A large class of non-smooth practical optimization problems can be written as minimization of a sum of smooth and partly smooth functions. We consider such structured problems which also depend on a parameter vector and study the problem of differentiating its solution mapping with respect to the parameter which has far reaching applications in sensitivity analysis and parameter learning optmization problems. We show that under partial smoothness and other mild assumptions, Automatic Differentiation (AD) of the sequence generated by proximal splitting algorithms converges to the derivative of the solution mapping. For a variant of automatic differentiation, which we call Fixed-Point Automatic Differentiation (FPAD), we remedy the memory overhead problem of the Reverse Mode AD and moreover provide faster convergence theoretically. We numerically illustrate the convergence and convergence rates of AD and FPAD on Lasso and Group Lasso problems and demonstrate the working of FPAD on prototypical practical image denoising problem by learning the regularization term.