Learning Invariant Subspaces of Koopman Operators--Part 2: Heterogeneous Dictionary Mixing to Approximate Subspace Invariance

This work builds on the models and concepts presented in part 1 to learn approximate dictionary representations of Koopman operators from data. Part I of this paper presented a methodology for arguing the subspace invariance of a Koopman dictionary. This methodology was demonstrated on the state-inclusive logistic lifting (SILL) basis. This is an affine basis augmented with conjunctive logistic functions. The SILL dictionary's nonlinear functions are homogeneous, a norm in data-driven dictionary learning of Koopman operators. In this paper, we discover that structured mixing of heterogeneous dictionary functions drawn from different classes of nonlinear functions achieve the same accuracy and dimensional scaling as the deep-learning-based deepDMD algorithm. We specifically show this by building a heterogeneous dictionary comprised of SILL functions and conjunctive radial basis functions (RBFs). This mixed dictionary achieves the same accuracy and dimensional scaling as deepDMD with an order of magnitude reduction in parameters, while maintaining geometric interpretability. These results strengthen the viability of dictionary-based Koopman models to solving high-dimensional nonlinear learning problems.

Learning Invariant Subspaces of Koopman Operators--Part 1: A Methodology for Demonstrating a Dictionary's Approximate Subspace Invariance

Koopman operators model nonlinear dynamics as a linear dynamic system acting on a nonlinear function as the state. This nonstandard state is often called a Koopman observable and is usually approximated numerically by a superposition of functions drawn from a dictionary. In a widely used algorithm, Extended Dynamic Mode Decomposition, the dictionary functions are drawn from a fixed class of functions. Recently, deep learning combined with EDMD has been used to learn novel dictionary functions in an algorithm called deep dynamic mode decomposition (deepDMD). The learned representation both (1) accurately models and (2) scales well with the dimension of the original nonlinear system. In this paper we analyze the learned dictionaries from deepDMD and explore the theoretical basis for their strong performance. We explore State-Inclusive Logistic Lifting (SILL) dictionary functions to approximate Koopman observables. Error analysis of these dictionary functions show they satisfy a property of subspace approximation, which we define as uniform finite approximate closure. Our results provide a hypothesis to explain the success of deep neural networks in learning numerical approximations to Koopman operators. Part 2 of this paper will extend this explanation by demonstrating the subspace invariant of heterogeneous dictionaries and presenting a head-to-head numerical comparison of deepDMD and low-parameter heterogeneous dictionary learning.

Heterogeneous mixtures of dictionary functions to approximate subspace invariance in Koopman operators

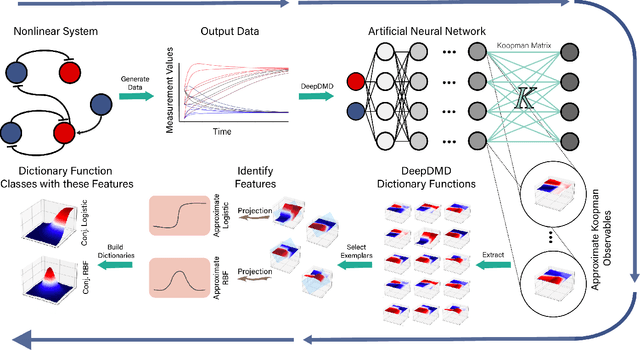
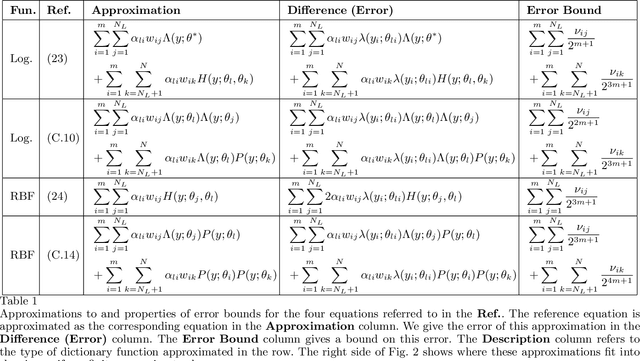
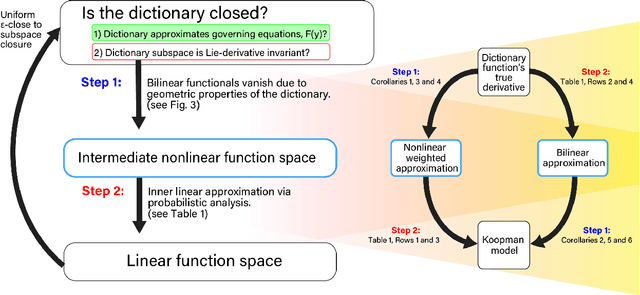
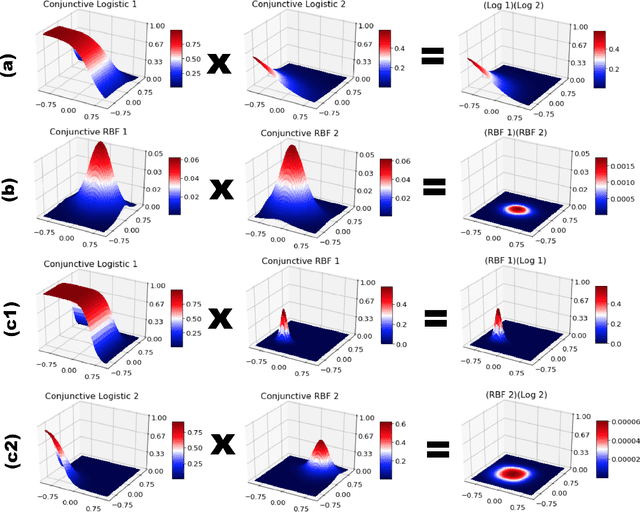
Koopman operators model nonlinear dynamics as a linear dynamic system acting on a nonlinear function as the state. This nonstandard state is often called a Koopman observable and is usually approximated numerically by a superposition of functions drawn from a \textit{dictionary}. A widely used algorithm, is \textit{Extended Dynamic Mode Decomposition}, where the dictionary functions are drawn from a fixed, homogeneous class of functions. Recently, deep learning combined with EDMD has been used to learn novel dictionary functions in an algorithm called deep dynamic mode decomposition (deepDMD). The learned representation both (1) accurately models and (2) scales well with the dimension of the original nonlinear system. In this paper we analyze the learned dictionaries from deepDMD and explore the theoretical basis for their strong performance. We discover a novel class of dictionary functions to approximate Koopman observables. Error analysis of these dictionary functions show they satisfy a property of subspace approximation, which we define as uniform finite approximate closure. We discover that structured mixing of heterogeneous dictionary functions drawn from different classes of nonlinear functions achieve the same accuracy and dimensional scaling as deepDMD. This mixed dictionary does so with an order of magnitude reduction in parameters, while maintaining geometric interpretability. Our results provide a hypothesis to explain the success of deep neural networks in learning numerical approximations to Koopman operators.