Shaolin Ji
A deep learning method for solving stochastic optimal control problems driven by fully-coupled FBSDEs
Apr 12, 2022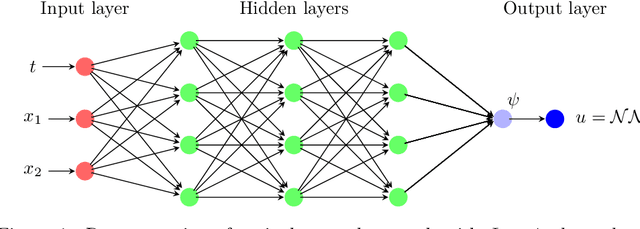
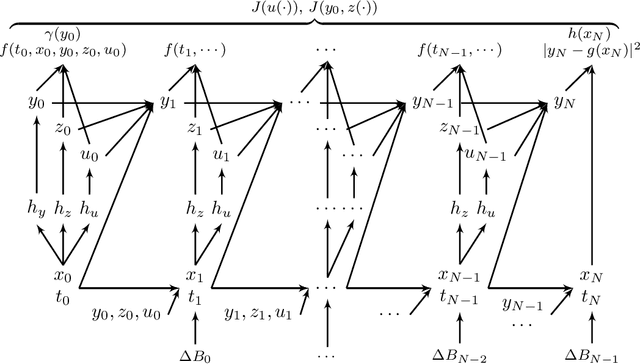
Abstract:In this paper, we mainly focus on the numerical solution of high-dimensional stochastic optimal control problem driven by fully-coupled forward-backward stochastic differential equations (FBSDEs in short) through deep learning. We first transform the problem into a stochastic Stackelberg differential game(leader-follower problem), then a cross-optimization method (CO method) is developed where the leader's cost functional and the follower's cost functional are optimized alternatively via deep neural networks. As for the numerical results, we compute two examples of the investment-consumption problem solved through stochastic recursive utility models, and the results of both examples demonstrate the effectiveness of our proposed algorithm.
A control method for solving high-dimensional Hamiltonian systems through deep neural networks
Nov 04, 2021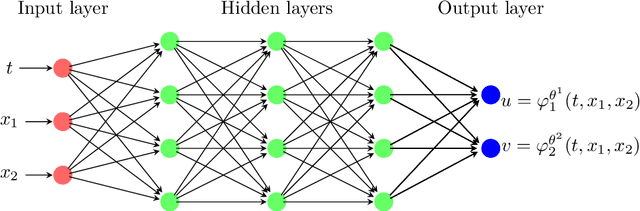
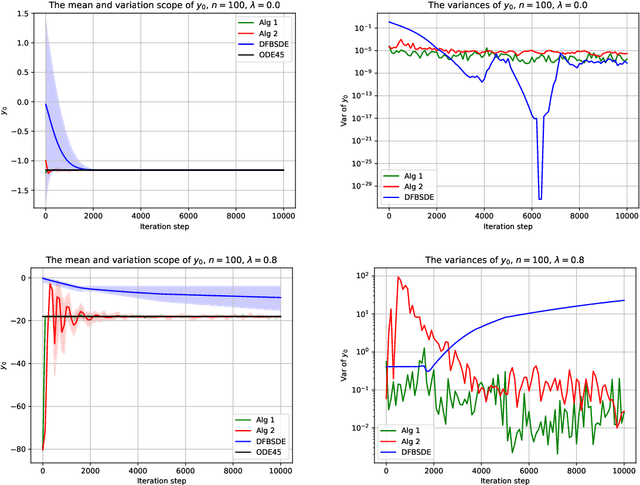
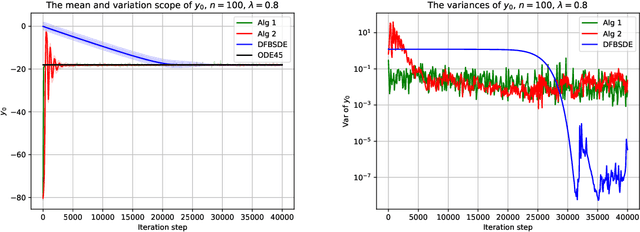
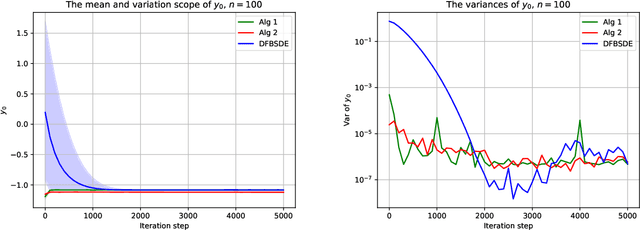
Abstract:In this paper, we mainly focus on solving high-dimensional stochastic Hamiltonian systems with boundary condition, and propose a novel method from the view of the stochastic control. In order to obtain the approximated solution of the Hamiltonian system, we first introduce a corresponding stochastic optimal control problem such that the Hamiltonian system of control problem is exactly what we need to solve, then develop two different algorithms suitable for different cases of the control problem and approximate the stochastic control via deep neural networks. From the numerical results, comparing with the Deep FBSDE method which was developed previously from the view of solving FBSDEs, the novel algorithms converge faster, which means that they require fewer training steps, and demonstrate more stable convergences for different Hamiltonian systems.
Deep learning method for solving stochastic optimal control problem via stochastic maximum principle
Jul 05, 2020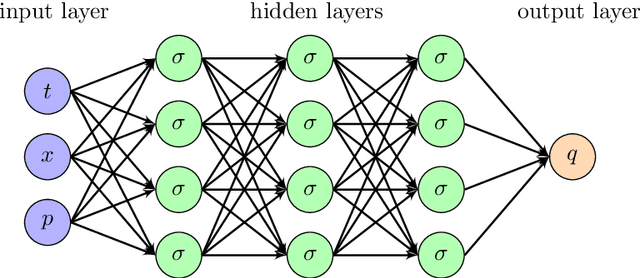

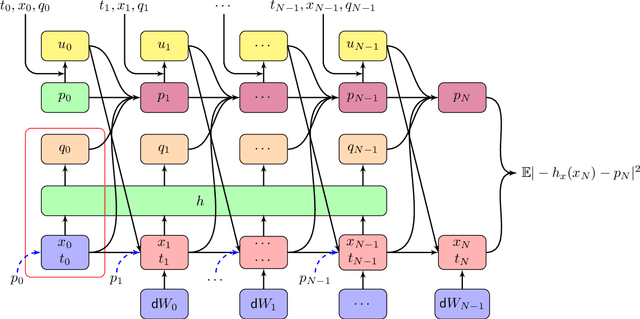
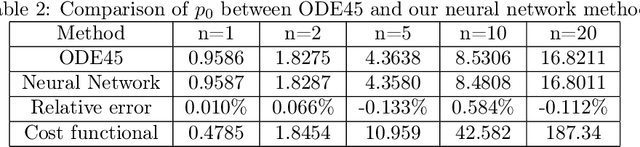
Abstract:In this paper, we aim to solve the stochastic optimal control problem via deep learning. Through the stochastic maximum principle and its corresponding Hamiltonian system, we propose a framework in which the original control problem is reformulated as a new one. This new stochastic optimal control problem has a quadratic loss function at the terminal time which provides an easier way to build a neural network structure. But the cost is that we must deal with an additional maximum condition. Some numerical examples such as the linear quadratic (LQ) stochastic optimal control problem and the calculation of G-expectation have been studied.
Three algorithms for solving high-dimensional fully-coupled FBSDEs through deep learning
Jul 17, 2019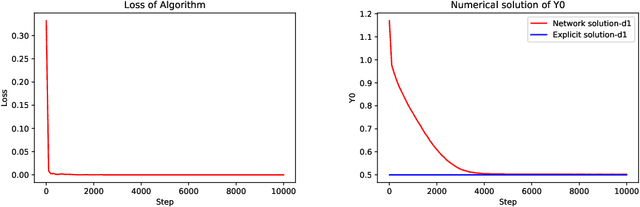
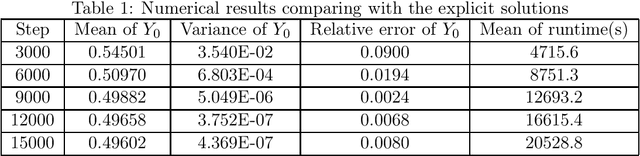
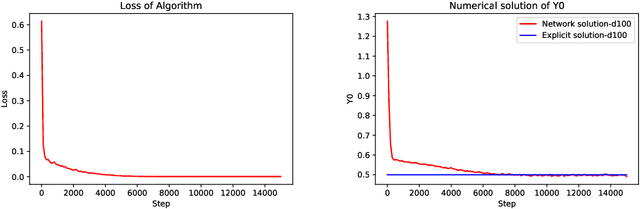
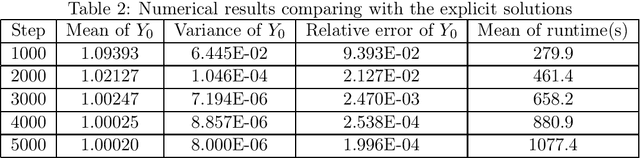
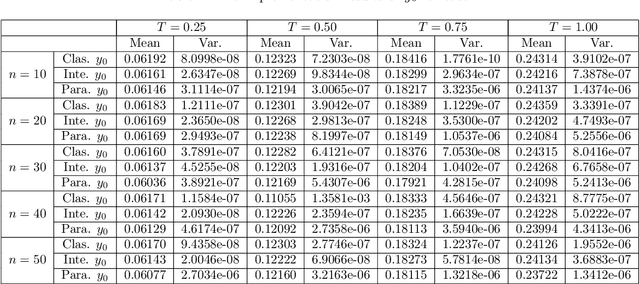
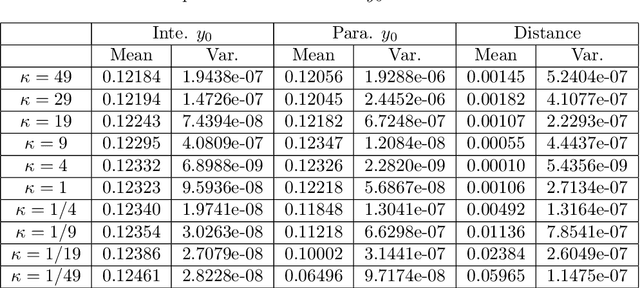
Abstract:Recently, the deep learning method has been used for solving forward backward stochastic differential equations (FBSDEs) and parabolic partial differential equations (PDEs). It has good accuracy and performance for high-dimensional problems. In this paper, we mainly solve fully coupled FBSDEs through deep learning and provide three algorithms. Several numerical results show remarkable performance especially for high-dimensional cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge