Deep learning method for solving stochastic optimal control problem via stochastic maximum principle

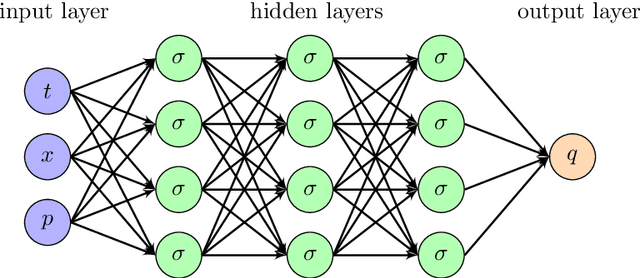
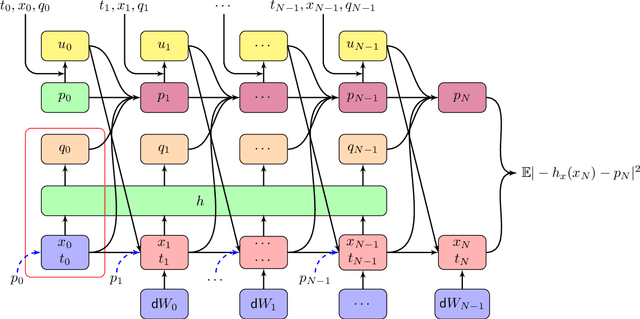
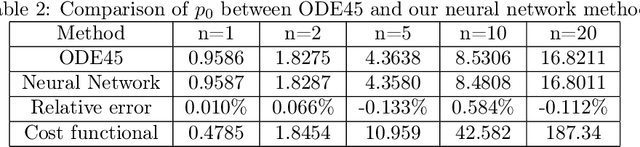
In this paper, we aim to solve the stochastic optimal control problem via deep learning. Through the stochastic maximum principle and its corresponding Hamiltonian system, we propose a framework in which the original control problem is reformulated as a new one. This new stochastic optimal control problem has a quadratic loss function at the terminal time which provides an easier way to build a neural network structure. But the cost is that we must deal with an additional maximum condition. Some numerical examples such as the linear quadratic (LQ) stochastic optimal control problem and the calculation of G-expectation have been studied.