Random Context and Semi-Conditional Insertion-Deletion Systems

In this article we introduce the operations of insertion and deletion working in a random-context and semi-conditional manner. We show that the conditional use of rules strictly increase the computational power. In the case of semi-conditional insertion-deletion systems context-free insertion and deletion rules of one symbol are sufficient to get the computational completeness. In the random context case our results expose an asymmetry between the computational power of insertion and deletion rules: systems of size $(2,0,0; 1,1,0)$ are computationally complete, while systems of size $(1,1,0;2,0,0)$ (and more generally of size $(1,1,0;p,1,1)$) are not. This is particularly interesting because other control mechanisms like graph-control or matrix control used together with insertion-deletion systems do not present such asymmetry.

Matrix Insertion-Deletion Systems

In this article, we consider for the first time the operations of insertion and deletion working in a matrix controlled manner. We show that, similarly as in the case of context-free productions, the computational power is strictly increased when using a matrix control: computational completeness can be obtained by systems with insertion or deletion rules involving at most two symbols in a contextual or in a context-free manner and using only binary matrices.

Minimization Strategies for Maximally Parallel Multiset Rewriting Systems

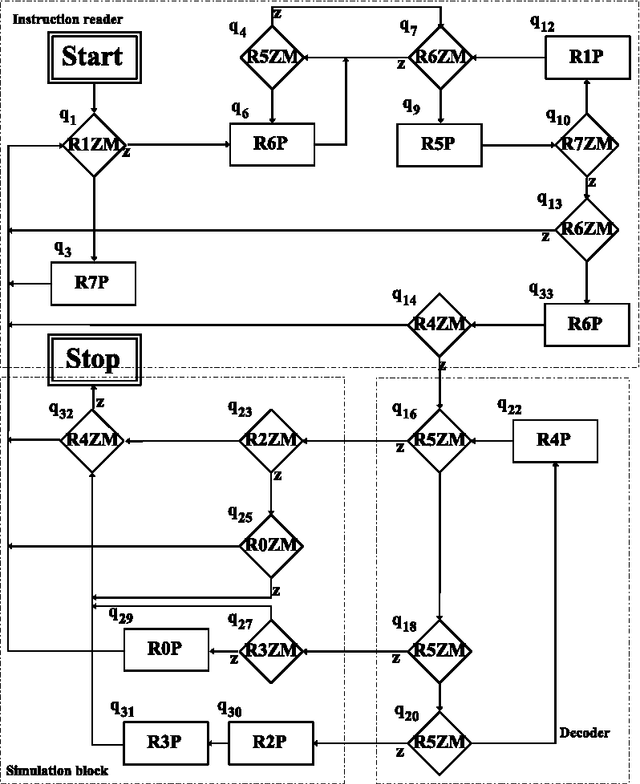
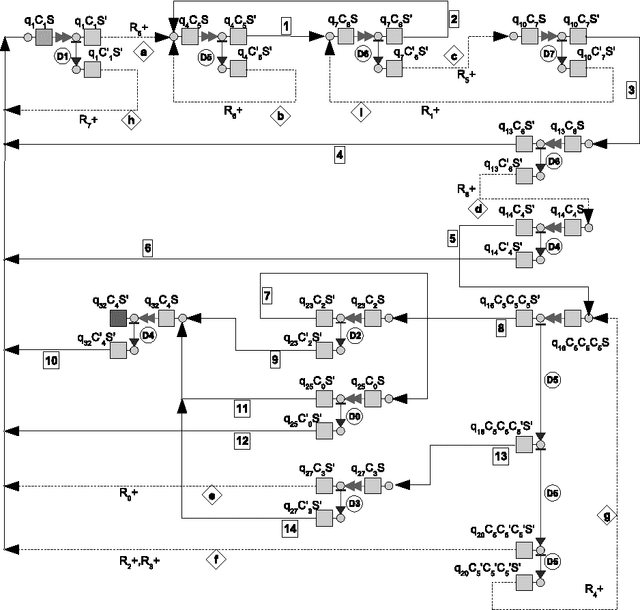
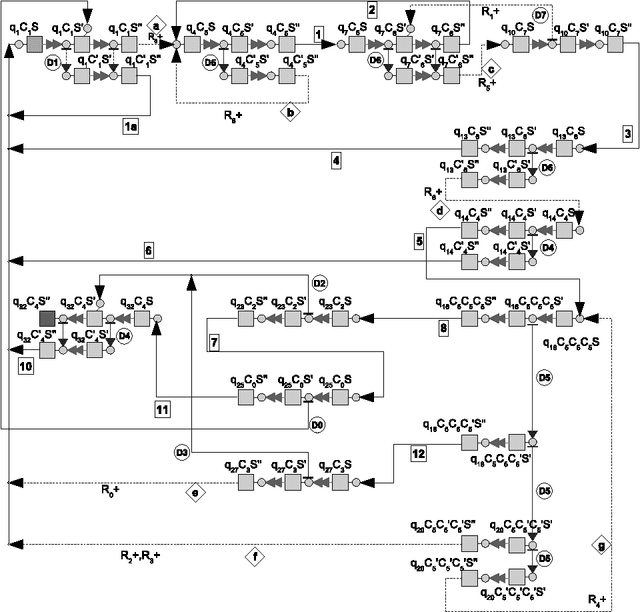
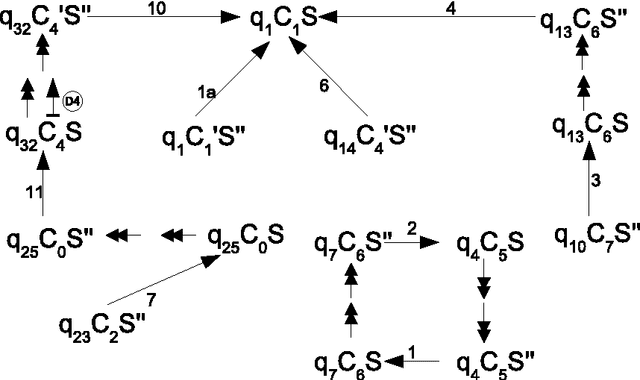
Maximally parallel multiset rewriting systems (MPMRS) give a convenient way to express relations between unstructured objects. The functioning of various computational devices may be expressed in terms of MPMRS (e.g., register machines and many variants of P systems). In particular, this means that MPMRS are computationally complete; however, a direct translation leads to quite a big number of rules. Like for other classes of computationally complete devices, there is a challenge to find a universal system having the smallest number of rules. In this article we present different rule minimization strategies for MPMRS based on encodings and structural transformations. We apply these strategies to the translation of a small universal register machine (Korec, 1996) and we show that there exists a universal MPMRS with 23 rules. Since MPMRS are identical to a restricted variant of P systems with antiport rules, the results we obtained improve previously known results on the number of rules for those systems.