Artiom Alhazov
Minimization Strategies for Maximally Parallel Multiset Rewriting Systems
Sep 14, 2010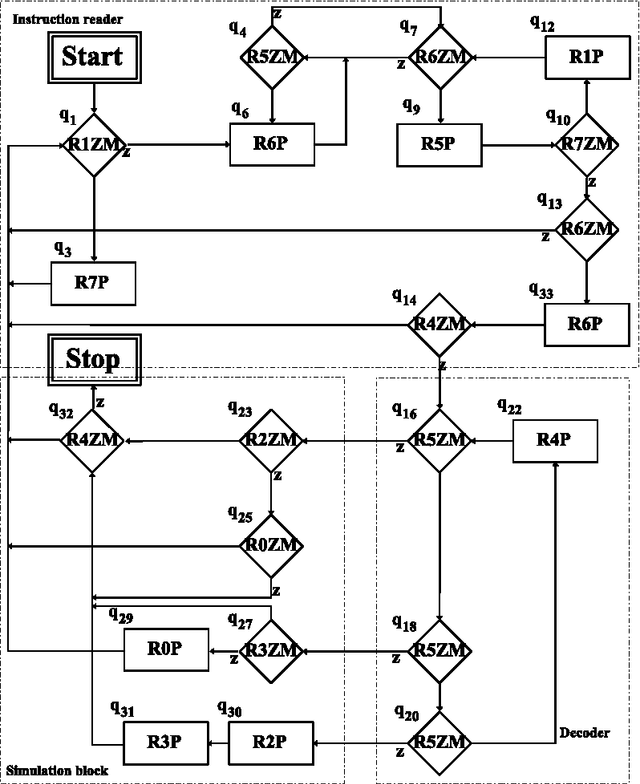
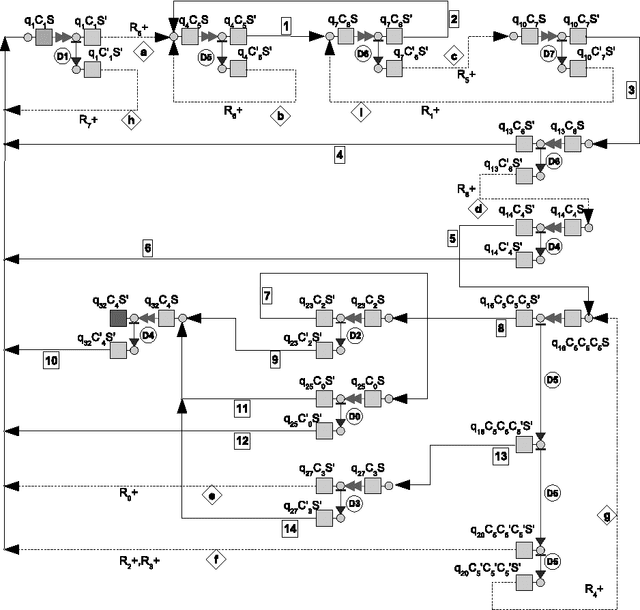
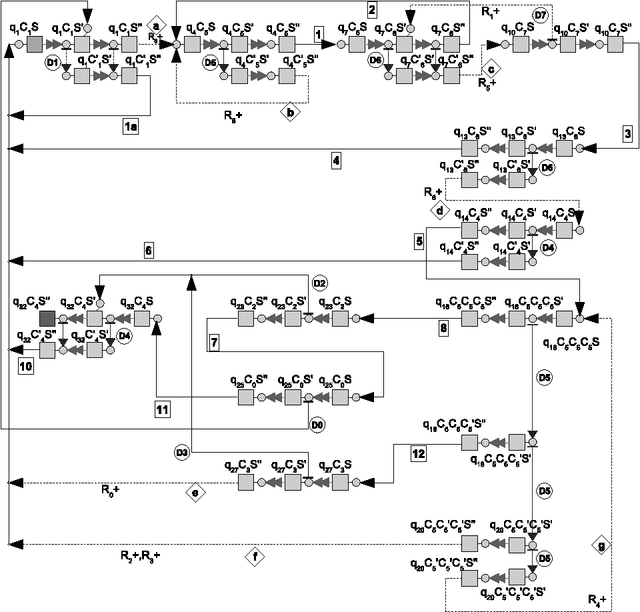
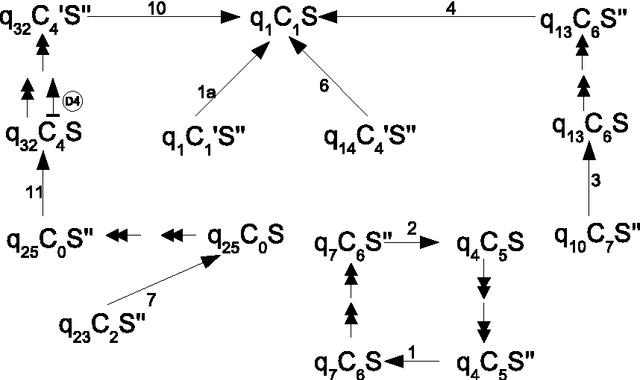
Abstract:Maximally parallel multiset rewriting systems (MPMRS) give a convenient way to express relations between unstructured objects. The functioning of various computational devices may be expressed in terms of MPMRS (e.g., register machines and many variants of P systems). In particular, this means that MPMRS are computationally complete; however, a direct translation leads to quite a big number of rules. Like for other classes of computationally complete devices, there is a challenge to find a universal system having the smallest number of rules. In this article we present different rule minimization strategies for MPMRS based on encodings and structural transformations. We apply these strategies to the translation of a small universal register machine (Korec, 1996) and we show that there exists a universal MPMRS with 23 rules. Since MPMRS are identical to a restricted variant of P systems with antiport rules, the results we obtained improve previously known results on the number of rules for those systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge