Serge Vicente
Determinantal consensus clustering
Feb 07, 2021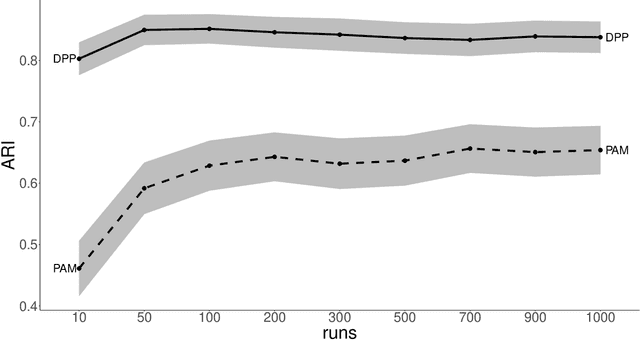
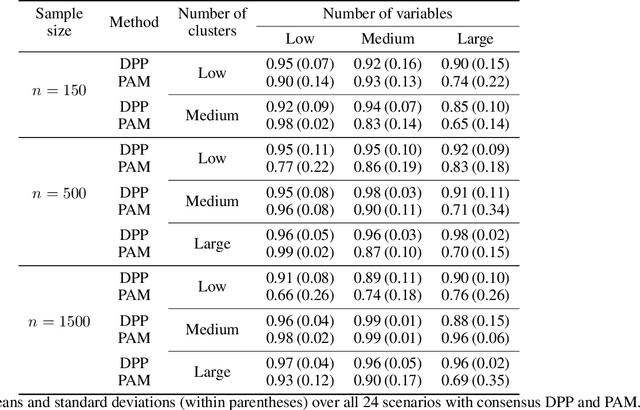
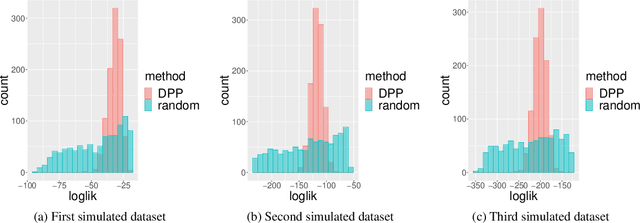
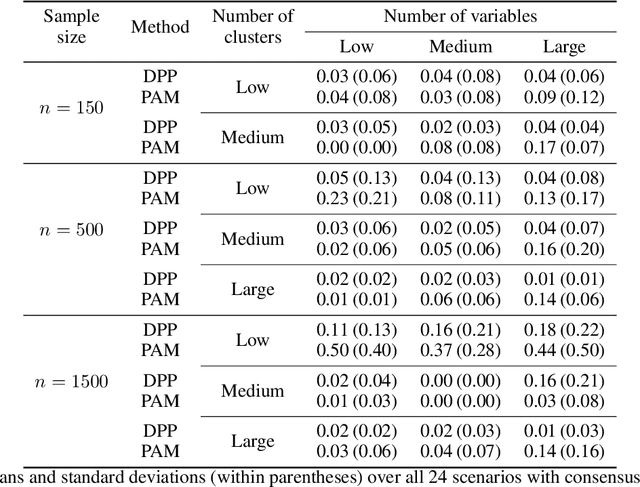
Abstract:Random restart of a given algorithm produces many partitions to yield a consensus clustering. Ensemble methods such as consensus clustering have been recognized as more robust approaches for data clustering than single clustering algorithms. We propose the use of determinantal point processes or DPP for the random restart of clustering algorithms based on initial sets of center points, such as k-medoids or k-means. The relation between DPP and kernel-based methods makes DPPs suitable to describe and quantify similarity between objects. DPPs favor diversity of the center points within subsets. So, subsets with more similar points have less chances of being generated than subsets with very distinct points. The current and most popular sampling technique is sampling center points uniformly at random. We show through extensive simulations that, contrary to DPP, this technique fails both to ensure diversity, and to obtain a good coverage of all data facets. These two properties of DPP are key to make DPPs achieve good performance with small ensembles. Simulations with artificial datasets and applications to real datasets show that determinantal consensus clustering outperform classical algorithms such as k-medoids and k-means consensus clusterings which are based on uniform random sampling of center points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge