Advanced Graph Clustering Methods: A Comprehensive and In-Depth Analysis

Graph clustering, which aims to divide a graph into several homogeneous groups, is a critical area of study with applications that span various fields such as social network analysis, bioinformatics, and image segmentation. This paper explores both traditional and more recent approaches to graph clustering. Firstly, key concepts and definitions in graph theory are introduced. The background section covers essential topics, including graph Laplacians and the integration of Deep Learning in graph analysis. The paper then delves into traditional clustering methods, including Spectral Clustering and the Leiden algorithm. Following this, state-of-the-art clustering techniques that leverage deep learning are examined. A comprehensive comparison of these methods is made through experiments. The paper concludes with a discussion of the practical applications of graph clustering and potential future research directions.

Probabilistic Auto-Associative Models and Semi-Linear PCA

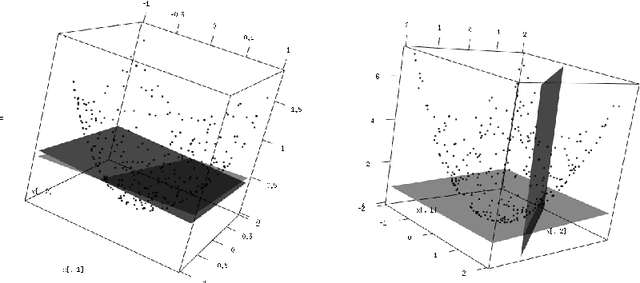
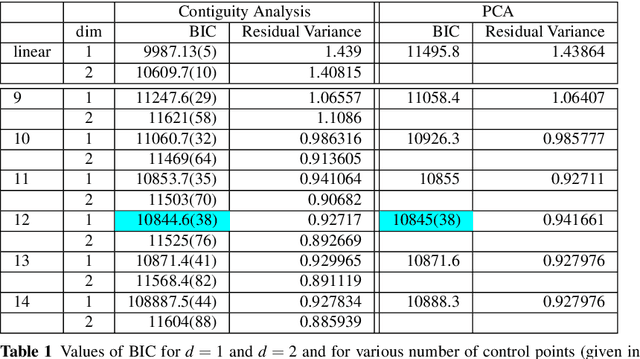
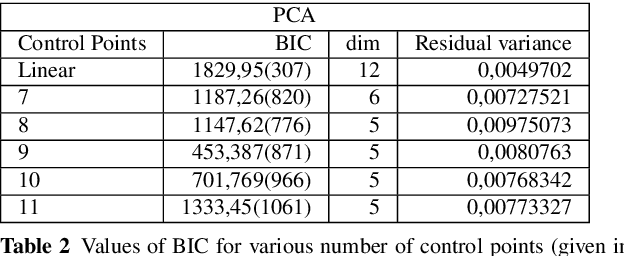
Auto-Associative models cover a large class of methods used in data analysis. In this paper, we describe the generals properties of these models when the projection component is linear and we propose and test an easy to implement Probabilistic Semi-Linear Auto- Associative model in a Gaussian setting. We show it is a generalization of the PCA model to the semi-linear case. Numerical experiments on simulated datasets and a real astronomical application highlight the interest of this approach

Auto-associative models, nonlinear Principal component analysis, manifolds and projection pursuit

In this paper, auto-associative models are proposed as candidates to the generalization of Principal Component Analysis. We show that these models are dedicated to the approximation of the dataset by a manifold. Here, the word "manifold" refers to the topology properties of the structure. The approximating manifold is built by a projection pursuit algorithm. At each step of the algorithm, the dimension of the manifold is incremented. Some theoretical properties are provided. In particular, we can show that, at each step of the algorithm, the mean residuals norm is not increased. Moreover, it is also established that the algorithm converges in a finite number of steps. Some particular auto-associative models are exhibited and compared to the classical PCA and some neural networks models. Implementation aspects are discussed. We show that, in numerous cases, no optimization procedure is required. Some illustrations on simulated and real data are presented.