Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence (1998)

This is the Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence, which was held in Madison, WI, July 24-26, 1998

Combination of Upper and Lower Probabilities

In this paper, we consider several types of information and methods of combination associated with incomplete probabilistic systems. We discriminate between 'a priori' and evidential information. The former one is a description of the whole population, the latest is a restriction based on observations for a particular case. Then, we propose different combination methods for each one of them. We also consider conditioning as the heterogeneous combination of 'a priori' and evidential information. The evidential information is represented as a convex set of likelihood functions. These will have an associated possibility distribution with behavior according to classical Possibility Theory.

Calculating Uncertainty Intervals From Conditional Convex Sets of Probabilities

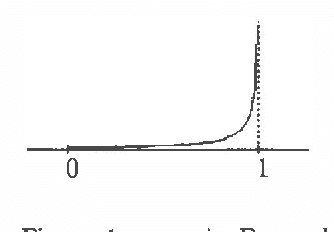
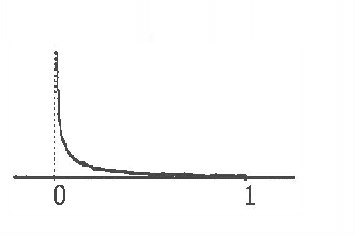
In Moral, Campos (1991) and Cano, Moral, Verdegay-Lopez (1991) a new method of conditioning convex sets of probabilities has been proposed. The result of it is a convex set of non-necessarily normalized probability distributions. The normalizing factor of each probability distribution is interpreted as the possibility assigned to it by the conditioning information. From this, it is deduced that the natural value for the conditional probability of an event is a possibility distribution. The aim of this paper is to study methods of transforming this possibility distribution into a probability (or uncertainty) interval. These methods will be based on the use of Sugeno and Choquet integrals. Their behaviour will be compared in basis to some selected examples.

Partially Specified Belief Functions

This paper presents a procedure to determine a complete belief function from the known values of belief for some of the subsets of the frame of discerment. The method is based on the principle of minimum commitment and a new principle called the focusing principle. This additional principle is based on the idea that belief is specified for the most relevant sets: the focal elements. The resulting procedure is compared with existing methods of building complete belief functions: the minimum specificity principle and the least commitment principle.

Independence Concepts for Convex Sets of Probabilities

In this paper we study different concepts of independence for convex sets of probabilities. There will be two basic ideas for independence. The first is irrelevance. Two variables are independent when a change on the knowledge about one variable does not affect the other. The second one is factorization. Two variables are independent when the joint convex set of probabilities can be decomposed on the product of marginal convex sets. In the case of the Theory of Probability, these two starting points give rise to the same definition. In the case of convex sets of probabilities, the resulting concepts will be strongly related, but they will not be equivalent. As application of the concept of independence, we shall consider the problem of building a global convex set from marginal convex sets of probabilities.

Inference with Idempotent Valuations

Valuation based systems verifying an idempotent property are studied. A partial order is defined between the valuations giving them a lattice structure. Then, two different strategies are introduced to represent valuations: as infimum of the most informative valuations or as supremum of the least informative ones. It is studied how to carry out computations with both representations in an efficient way. The particular cases of finite sets and convex polytopes are considered.