How more data can hurt: Instability and regularization in next-generation reservoir computing

It has been found recently that more data can, counter-intuitively, hurt the performance of deep neural networks. Here, we show that a more extreme version of the phenomenon occurs in data-driven models of dynamical systems. To elucidate the underlying mechanism, we focus on next-generation reservoir computing (NGRC) -- a popular framework for learning dynamics from data. We find that, despite learning a better representation of the flow map with more training data, NGRC can adopt an ill-conditioned ``integrator'' and lose stability. We link this data-induced instability to the auxiliary dimensions created by the delayed states in NGRC. Based on these findings, we propose simple strategies to mitigate the instability, either by increasing regularization strength in tandem with data size, or by carefully introducing noise during training. Our results highlight the importance of proper regularization in data-driven modeling of dynamical systems.

Mastering Percolation-like Games with Deep Learning

Though robustness of networks to random attacks has been widely studied, intentional destruction by an intelligent agent is not tractable with previous methods. Here we devise a single-player game on a lattice that mimics the logic of an attacker attempting to destroy a network. The objective of the game is to disable all nodes in the fewest number of steps. We develop a reinforcement learning approach using deep Q-learning that is capable of learning to play this game successfully, and in so doing, to optimally attack a network. Because the learning algorithm is universal, we train agents on different definitions of robustness and compare the learned strategies. We find that superficially similar definitions of robustness induce different strategies in the trained agent, implying that optimally attacking or defending a network is sensitive the particular objective. Our method provides a new approach to understand network robustness, with potential applications to other discrete processes in disordered systems.

A Catch-22 of Reservoir Computing

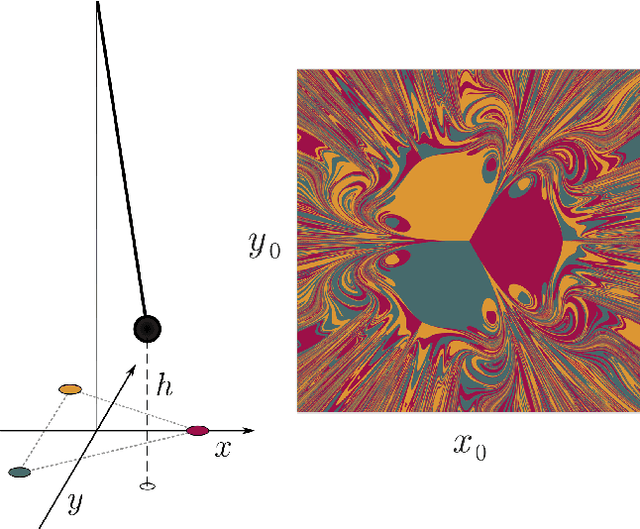
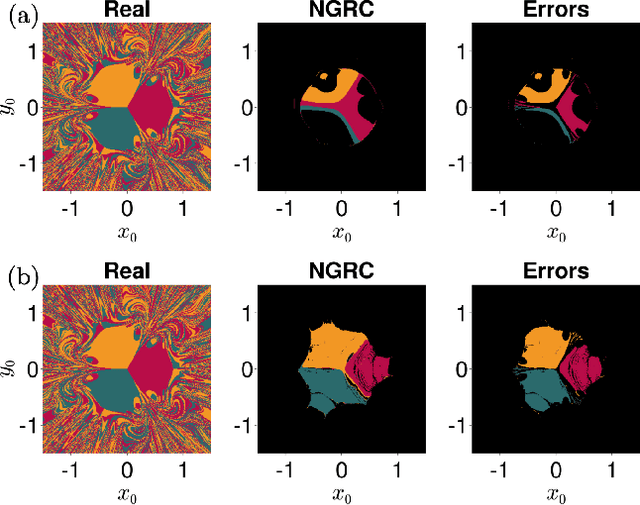
Reservoir Computing (RC) is a simple and efficient model-free framework for data-driven predictions of nonlinear dynamical systems. Recently, Next Generation Reservoir Computing (NGRC) has emerged as an especially attractive variant of RC. By shifting the nonlinearity from the reservoir to the readout layer, NGRC requires less data and has fewer hyperparameters to optimize, making it suitable for challenging tasks such as predicting basins of attraction. Here, using paradigmatic multistable systems including magnetic pendulums and coupled Kuramoto oscillators, we show that the performance of NGRC models can be extremely sensitive to the choice of readout nonlinearity. In particular, by incorporating the exact nonlinearity from the original equations, NGRC trained on a single trajectory can predict pseudo-fractal basins with almost perfect accuracy. However, even a small uncertainty on the exact nonlinearity can completely break NGRC, rendering the prediction accuracy no better than chance. This creates a catch-22 for NGRC since it may not be able to make useful predictions unless a key part of the system being predicted (i.e., its nonlinearity) is already known. Our results highlight the challenges faced by data-driven methods in learning complex dynamical systems.