A Catch-22 of Reservoir Computing
Paper and Code
Oct 18, 2022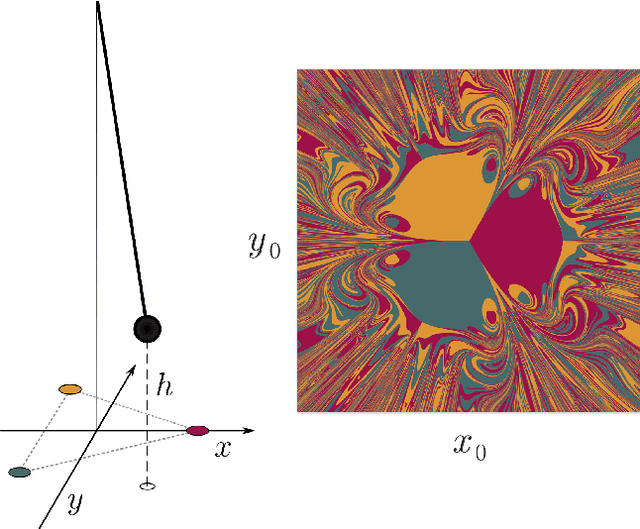
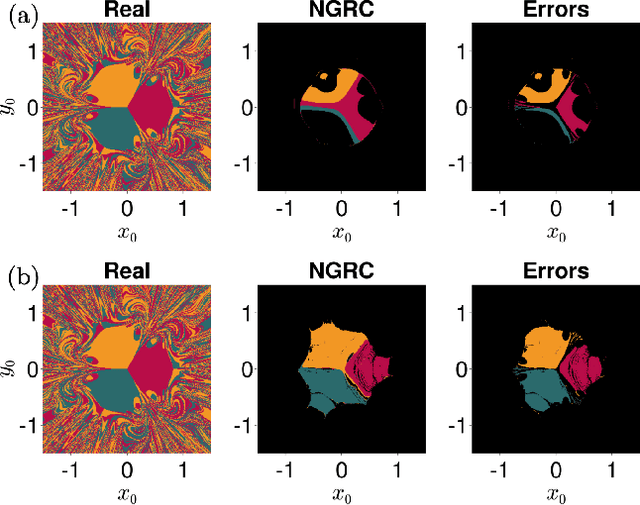


Reservoir Computing (RC) is a simple and efficient model-free framework for data-driven predictions of nonlinear dynamical systems. Recently, Next Generation Reservoir Computing (NGRC) has emerged as an especially attractive variant of RC. By shifting the nonlinearity from the reservoir to the readout layer, NGRC requires less data and has fewer hyperparameters to optimize, making it suitable for challenging tasks such as predicting basins of attraction. Here, using paradigmatic multistable systems including magnetic pendulums and coupled Kuramoto oscillators, we show that the performance of NGRC models can be extremely sensitive to the choice of readout nonlinearity. In particular, by incorporating the exact nonlinearity from the original equations, NGRC trained on a single trajectory can predict pseudo-fractal basins with almost perfect accuracy. However, even a small uncertainty on the exact nonlinearity can completely break NGRC, rendering the prediction accuracy no better than chance. This creates a catch-22 for NGRC since it may not be able to make useful predictions unless a key part of the system being predicted (i.e., its nonlinearity) is already known. Our results highlight the challenges faced by data-driven methods in learning complex dynamical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge