SDCOR: Scalable Density-based Clustering for Local Outlier Detection in Massive-Scale Datasets

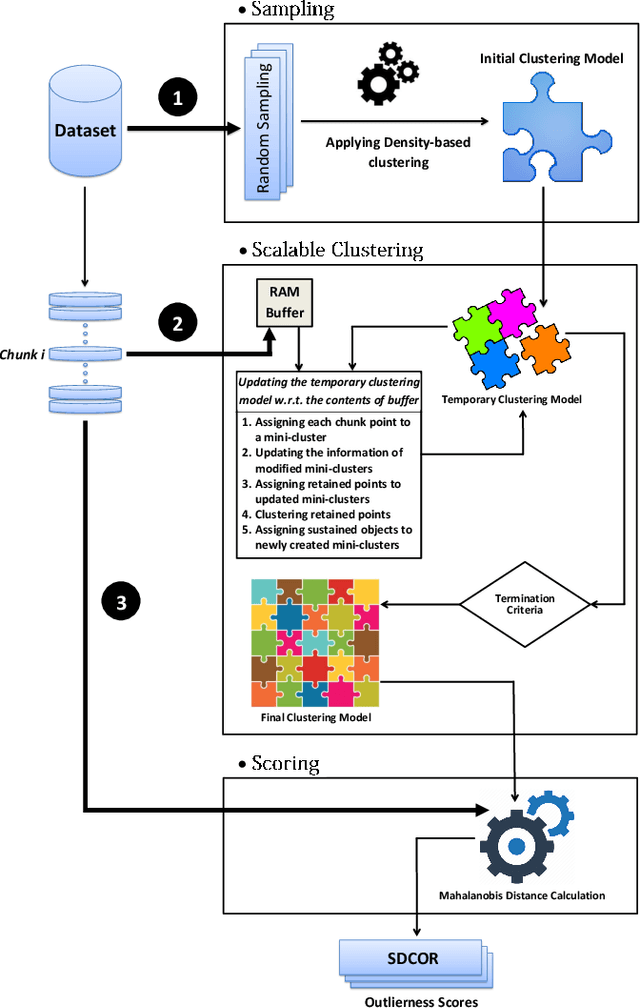
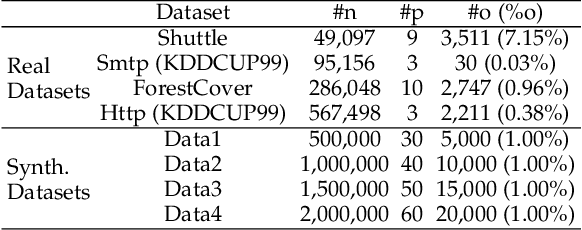
This paper presents a batch-wise density-based clustering approach for local outlier detection in massive-scale datasets. Differently from well-known traditional algorithms, which assume that all the data is memory-resident, our proposed method is scalable and processes the data chunk-by-chunk within the confines of a limited memory buffer. At first, a temporary clustering model is built, then it is incrementally updated by analyzing consecutive memory loads of points. Ultimately, the proposed algorithm will give an outlying score to each object, which is named SDCOR (Scalable Density-based Clustering Outlierness Ratio). Evaluations on real-life and synthetic datasets demonstrate that the proposed method has a low linear time complexity and is more effective and efficient compared to best-known conventional density-based methods, which need to load all the data into memory; and also to some fast distance-based methods which can perform on the data resident in the disk.

A Grid-based Approach for Convexity Analysis of a Density-based Cluster

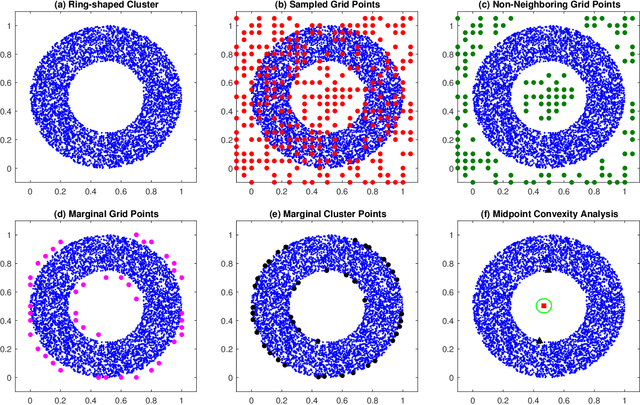
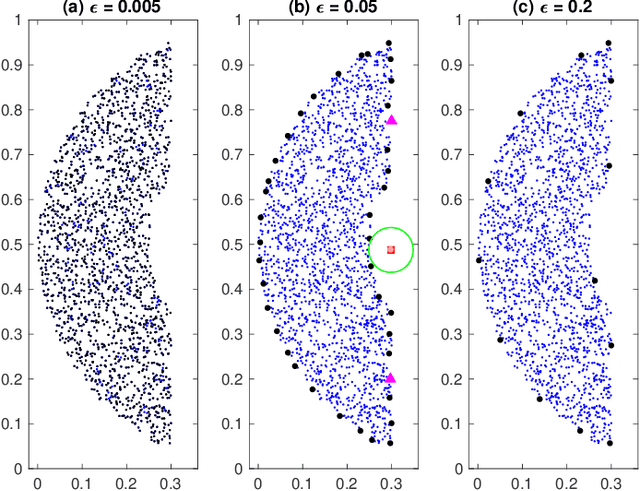
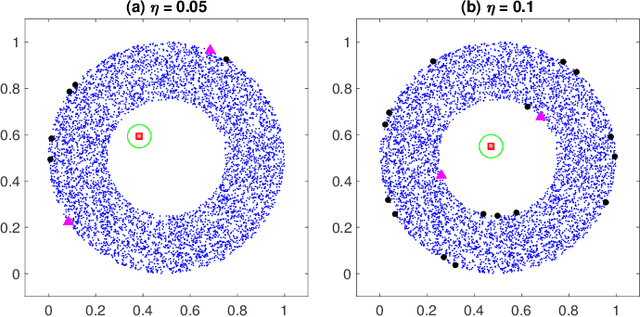
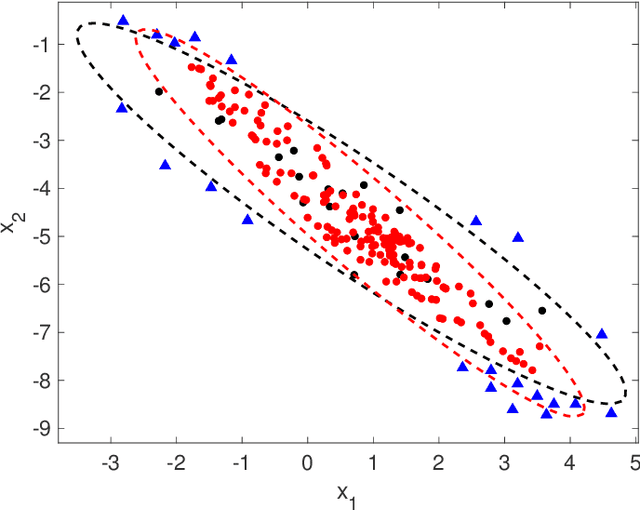
This paper presents a novel geometrical approach to investigate the convexity of a density-based cluster. Our approach is grid-based and we are about to calibrate the value space of the cluster. However, the cluster objects are coming from an infinite distribution, their number is finite, and thus, the regarding shape will not be sharp. Therefore, we establish the precision of the grid properly in a way that, the reliable approximate boundaries of the cluster are founded. After that, regarding the simple notion of convex sets and midpoint convexity, we investigate whether or not the density-based cluster is convex. Moreover, our experiments on synthetic datasets demonstrate the desirable performance of our method.