Signal-based online acceleration and strain data fusion using B-splines and Kalman filter for full-field dynamic displacement estimation

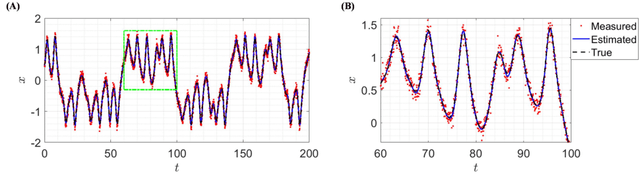
Displacement plays a crucial role in structural health monitoring (SHM) and damage detection of structural systems subjected to dynamic loads. However, due to the inconvenience associated with the direct measurement of displacement during dynamic loading and the high cost of displacement sensors, the use of displacement measurements often gets restricted. In recent years, indirect estimation of displacement from acceleration and strain data has gained popularity. Several researchers have developed data fusion techniques to estimate displacement from acceleration and strain data. However, existing data fusion techniques mostly rely on system properties like mode shapes or finite element models and require accurate knowledge about the system for successful implementation. Hence, they have the inherent limitation of their applicability being restricted to relatively simple structures where such information is easily available. In this article, B-spline basis functions have been used to formulate a Kalman filter-based algorithm for acceleration and strain data fusion using only elementary information about the system, such as the geometry and boundary conditions, which is the major advantage of this method. Also, the proposed algorithm enables us to monitor the full-field displacement of the system online with only a limited number of sensors. The method has been validated on a numerically generated dataset from the finite element model of a tapered beam subjected to dynamic excitation. Later, the proposed data fusion technique was applied to an experimental benchmark test of a wind turbine blade under dynamic load to estimate the displacement time history. In both cases, the reconstructed displacement from strain and acceleration was found to match well with the response from the FE model.

KAN/MultKAN with Physics-Informed Spline fitting (KAN-PISF) for ordinary/partial differential equation discovery of nonlinear dynamic systems

Machine learning for scientific discovery is increasingly becoming popular because of its ability to extract and recognize the nonlinear characteristics from the data. The black-box nature of deep learning methods poses difficulties in interpreting the identified model. There is a dire need to interpret the machine learning models to develop a physical understanding of dynamic systems. An interpretable form of neural network called Kolmogorov-Arnold networks (KAN) or Multiplicative KAN (MultKAN) offers critical features that help recognize the nonlinearities in the governing ordinary/partial differential equations (ODE/PDE) of various dynamic systems and find their equation structures. In this study, an equation discovery framework is proposed that includes i) sequentially regularized derivatives for denoising (SRDD) algorithm to denoise the measure data to obtain accurate derivatives, ii) KAN to identify the equation structure and suggest relevant nonlinear functions that are used to create a small overcomplete library of functions, and iii) physics-informed spline fitting (PISF) algorithm to filter the excess functions from the library and converge to the correct equation. The framework was tested on the forced Duffing oscillator, Van der Pol oscillator (stiff ODE), Burger's equation, and Bouc-Wen model (coupled ODE). The proposed method converged to the true equation for the first three systems. It provided an approximate model for the Bouc-Wen model that could acceptably capture the hysteresis response. Using KAN maintains low complexity, which helps the user interpret the results throughout the process and avoid the black-box-type nature of machine learning methods.

Physics-informed AI and ML-based sparse system identification algorithm for discovery of PDE's representing nonlinear dynamic systems

Sparse system identification of nonlinear dynamic systems is still challenging, especially for stiff and high-order differential equations for noisy measurement data. The use of highly correlated functions makes distinguishing between true and false functions difficult, which limits the choice of functions. In this study, an equation discovery method has been proposed to tackle these problems. The key elements include a) use of B-splines for data fitting to get analytical derivatives superior to numerical derivatives, b) sequentially regularized derivatives for denoising (SRDD) algorithm, highly effective in removing noise from signal without system information loss, c) uncorrelated component analysis (UCA) algorithm that identifies and eliminates highly correlated functions while retaining the true functions, and d) physics-informed spline fitting (PISF) where the spline fitting is updated gradually while satisfying the governing equation with a dictionary of candidate functions to converge to the correct equation sequentially. The complete framework is built on a unified deep-learning architecture that eases the optimization process. The proposed method is demonstrated to discover various differential equations at various noise levels, including three-dimensional, fourth-order, and stiff equations. The parameter estimation converges accurately to the true values with a small coefficient of variation, suggesting robustness to the noise.

Data-Driven Theory-guided Learning of Partial Differential Equations using SimultaNeous Basis Function Approximation and Parameter Estimation

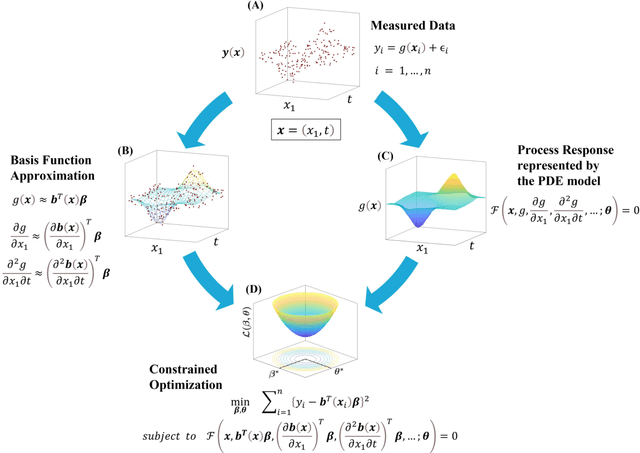
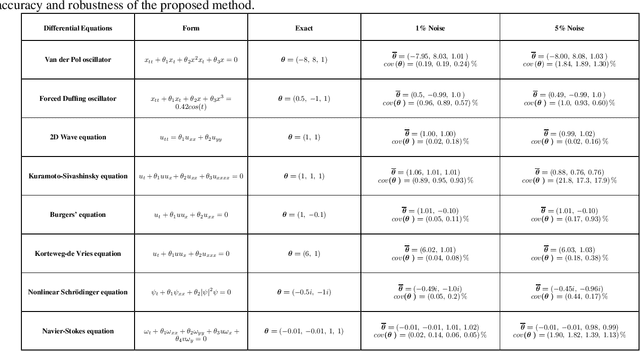
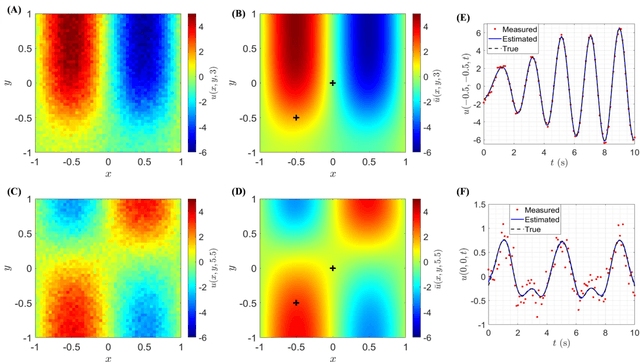
The measured spatiotemporal response of various physical processes is utilized to infer the governing partial differential equations (PDEs). We propose SimultaNeous Basis Function Approximation and Parameter Estimation (SNAPE), a technique of parameter estimation of PDEs that is robust against high levels of noise nearly 100 %, by simultaneously fitting basis functions to the measured response and estimating the parameters of both ordinary and partial differential equations. The domain knowledge of the general multidimensional process is used as a constraint in the formulation of the optimization framework. SNAPE not only demonstrates its applicability on various complex dynamic systems that encompass wide scientific domains including Schr\"odinger equation, chaotic duffing oscillator, and Navier-Stokes equation but also estimates an analytical approximation to the process response. The method systematically combines the knowledge of well-established scientific theories and the concepts of data science to infer the properties of the process from the observed data.