Data-Driven Theory-guided Learning of Partial Differential Equations using SimultaNeous Basis Function Approximation and Parameter Estimation

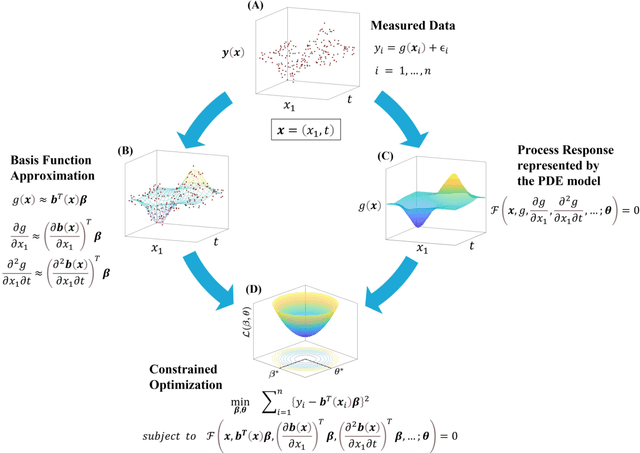
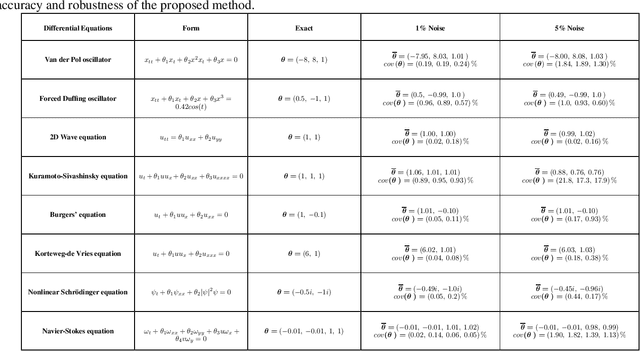
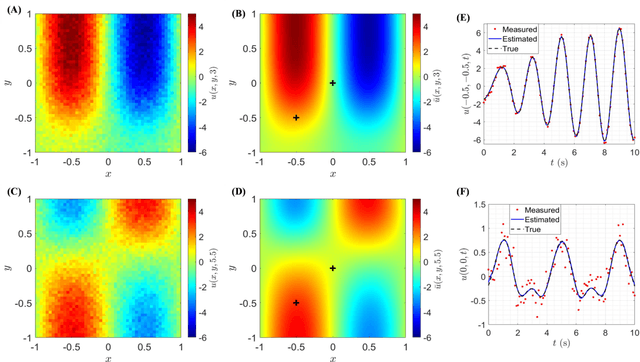
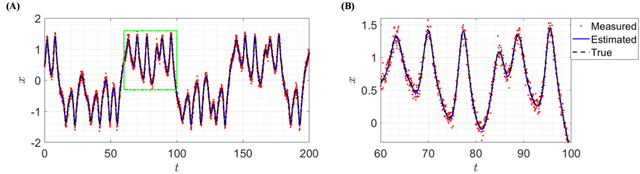
The measured spatiotemporal response of various physical processes is utilized to infer the governing partial differential equations (PDEs). We propose SimultaNeous Basis Function Approximation and Parameter Estimation (SNAPE), a technique of parameter estimation of PDEs that is robust against high levels of noise nearly 100 %, by simultaneously fitting basis functions to the measured response and estimating the parameters of both ordinary and partial differential equations. The domain knowledge of the general multidimensional process is used as a constraint in the formulation of the optimization framework. SNAPE not only demonstrates its applicability on various complex dynamic systems that encompass wide scientific domains including Schr\"odinger equation, chaotic duffing oscillator, and Navier-Stokes equation but also estimates an analytical approximation to the process response. The method systematically combines the knowledge of well-established scientific theories and the concepts of data science to infer the properties of the process from the observed data.