Secure Power Control for Downlink Cell-Free Massive MIMO With Passive Eavesdroppers

This work studies secure communications for a cell-free massive multiple-input multiple-output (CF-mMIMO) network which is attacked by multiple passive eavesdroppers overhearing communications between access points (APs) and users in the network. It will be revealed that the distributed APs in CF-mMIMO allows not only legitimate users but also eavesdroppers to reap the diversity gain, which seriously degrades secrecy performance. Motivated by this, this work proposes an artificial noise (AN)-aided secure power control scheme for CF-mMIMO under passive eavesdropping aiming to achieve a higher secrecy rate and/or guarantee security. In particular, it will be demonstrated that a careful use of AN signal in the power control is especially important to improve the secrecy performance. The performance of the proposed power control scheme is evaluated and compared with various power control schemes via numerical experiments, which clearly shows that the proposed power control scheme outperforms all the competing schemes.

Fast Federated Learning by Balancing Communication Trade-Offs

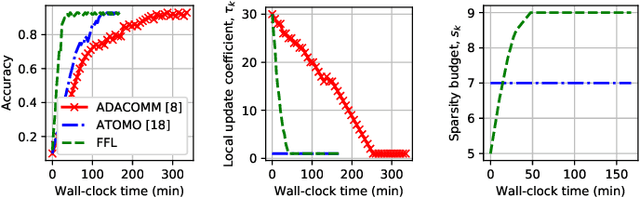
Federated Learning (FL) has recently received a lot of attention for large-scale privacy-preserving machine learning. However, high communication overheads due to frequent gradient transmissions decelerate FL. To mitigate the communication overheads, two main techniques have been studied: (i) local update of weights characterizing the trade-off between communication and computation and (ii) gradient compression characterizing the trade-off between communication and precision. To the best of our knowledge, studying and balancing those two trade-offs jointly and dynamically while considering their impacts on convergence has remained unresolved even though it promises significantly faster FL. In this paper, we first formulate our problem to minimize learning error with respect to two variables: local update coefficients and sparsity budgets of gradient compression who characterize trade-offs between communication and computation/precision, respectively. We then derive an upper bound of the learning error in a given wall-clock time considering the interdependency between the two variables. Based on this theoretical analysis, we propose an enhanced FL scheme, namely Fast FL (FFL), that jointly and dynamically adjusts the two variables to minimize the learning error. We demonstrate that FFL consistently achieves higher accuracies faster than similar schemes existing in the literature.