Salaheddin Alakkari
An Acceleration Scheme for Memory Limited, Streaming PCA
Jul 17, 2018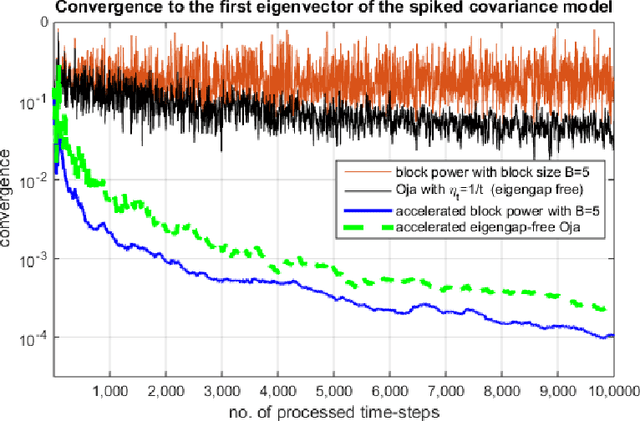
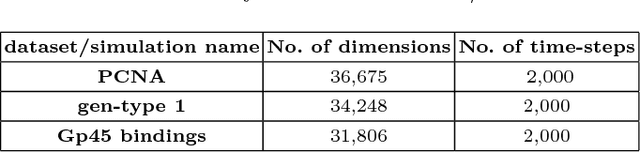
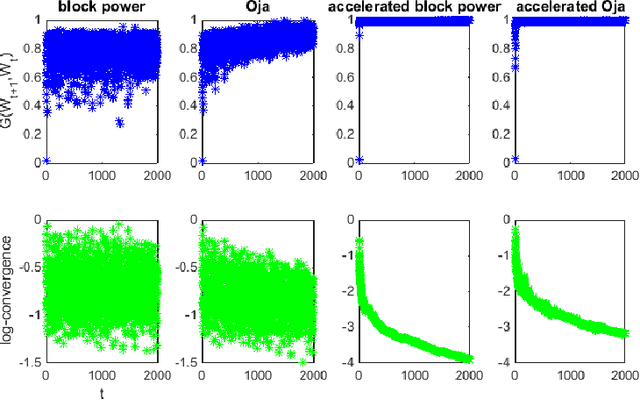
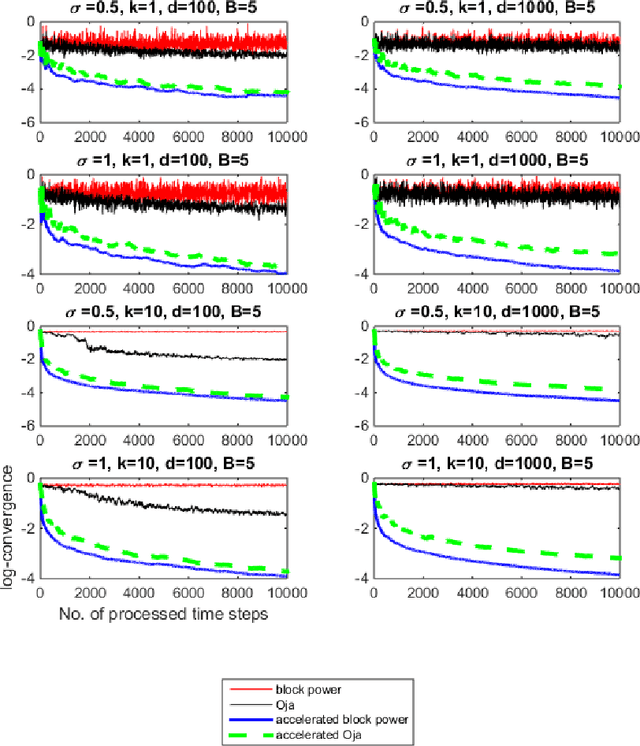
Abstract:In this paper, we propose an acceleration scheme for online memory-limited PCA methods. Our scheme converges to the first $k>1$ eigenvectors in a single data pass. We provide empirical convergence results of our scheme based on the spiked covariance model. Our scheme does not require any predefined parameters such as the eigengap and hence is well facilitated for streaming data scenarios. Furthermore, we apply our scheme to challenging time-varying systems where online PCA methods fail to converge. Specifically, we discuss a family of time-varying systems that are based on Molecular Dynamics simulations where batch PCA converges to the actual analytic solution of such systems.
Adaptive PCA for Time-Varying Data
Sep 12, 2017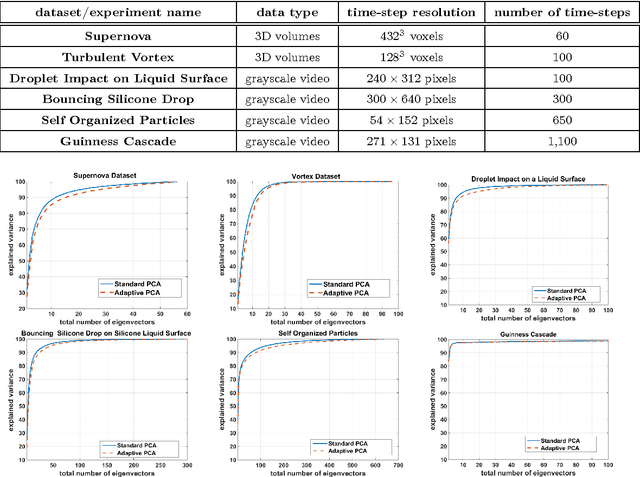
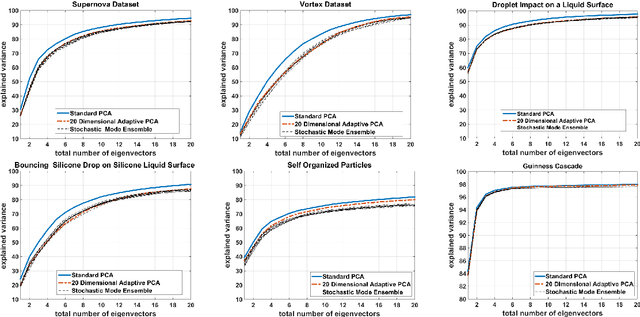
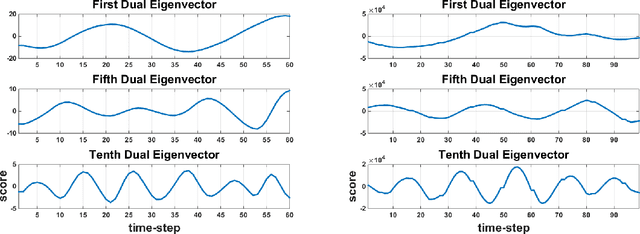
Abstract:In this paper, we present an online adaptive PCA algorithm that is able to compute the full dimensional eigenspace per new time-step of sequential data. The algorithm is based on a one-step update rule that considers all second order correlations between previous samples and the new time-step. Our algorithm has O(n) complexity per new time-step in its deterministic mode and O(1) complexity per new time-step in its stochastic mode. We test our algorithm on a number of time-varying datasets of different physical phenomena. Explained variance curves indicate that our technique provides an excellent approximation to the original eigenspace computed using standard PCA in batch mode. In addition, our experiments show that the stochastic mode, despite its much lower computational complexity, converges to the same eigenspace computed using the deterministic mode.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge