CrowdSplat: Exploring Gaussian Splatting For Crowd Rendering

We present CrowdSplat, a novel approach that leverages 3D Gaussian Splatting for real-time, high-quality crowd rendering. Our method utilizes 3D Gaussian functions to represent animated human characters in diverse poses and outfits, which are extracted from monocular videos. We integrate Level of Detail (LoD) rendering to optimize computational efficiency and quality. The CrowdSplat framework consists of two stages: (1) avatar reconstruction and (2) crowd synthesis. The framework is also optimized for GPU memory usage to enhance scalability. Quantitative and qualitative evaluations show that CrowdSplat achieves good levels of rendering quality, memory efficiency, and computational performance. Through these experiments, we demonstrate that CrowdSplat is a viable solution for dynamic, realistic crowd simulation in real-time applications.

Evaluating CrowdSplat: Perceived Level of Detail for Gaussian Crowds

Efficient and realistic crowd rendering is an important element of many real-time graphics applications such as Virtual Reality (VR) and games. To this end, Levels of Detail (LOD) avatar representations such as polygonal meshes, image-based impostors, and point clouds have been proposed and evaluated. More recently, 3D Gaussian Splatting has been explored as a potential method for real-time crowd rendering. In this paper, we present a two-alternative forced choice (2AFC) experiment that aims to determine the perceived quality of 3D Gaussian avatars. Three factors were explored: Motion, LOD (i.e., #Gaussians), and the avatar height in Pixels (corresponding to the viewing distance). Participants viewed pairs of animated 3D Gaussian avatars and were tasked with choosing the most detailed one. Our findings can inform the optimization of LOD strategies in Gaussian-based crowd rendering, thereby helping to achieve efficient rendering while maintaining visual quality in real-time applications.

Perceptually Optimized Color Selection for Visualization

We propose an approach, called the Equilibrium Distribution Model (EDM), for automatically selecting colors with optimum perceptual contrast for scientific visualization. Given any number of features that need to be emphasized in a visualization task, our approach derives evenly distributed points in the CIELAB color space to assign colors to the features so that the minimum Euclidean Distance among the colors are optimized. Our approach can assign colors with high perceptual contrast even for very high numbers of features, where other color selection methods typically fail. We compare our approach with the widely used Harmonic color selection scheme and demonstrate that while the harmonic scheme can achieve reasonable color contrast for visualizing up to 20 different features, our Equilibrium scheme provides significantly better contrast and achieves perceptible contrast for visualizing even up to 100 unique features.

An Acceleration Scheme for Memory Limited, Streaming PCA

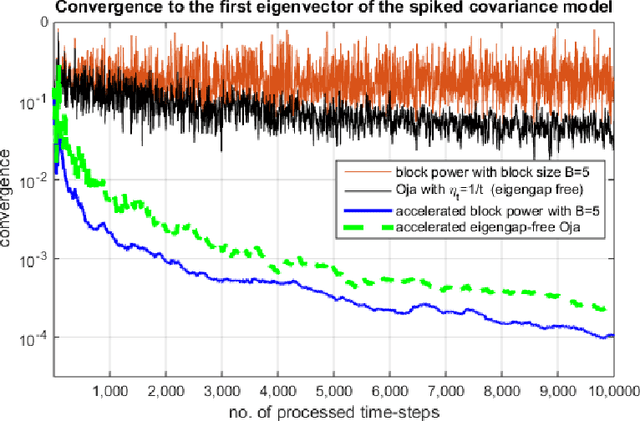
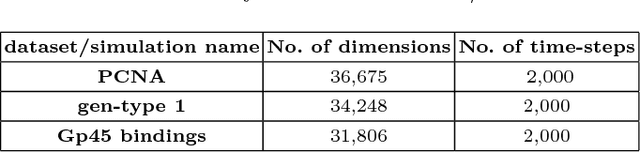
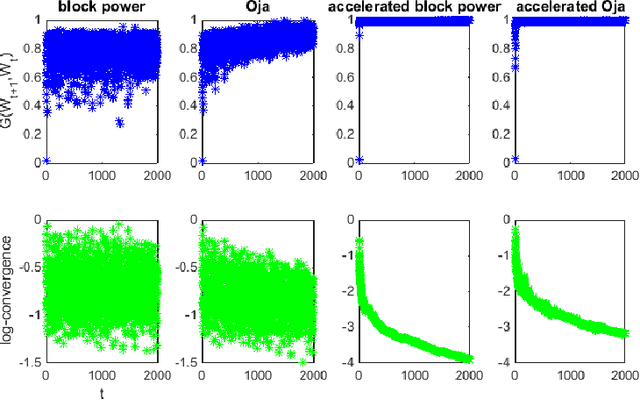
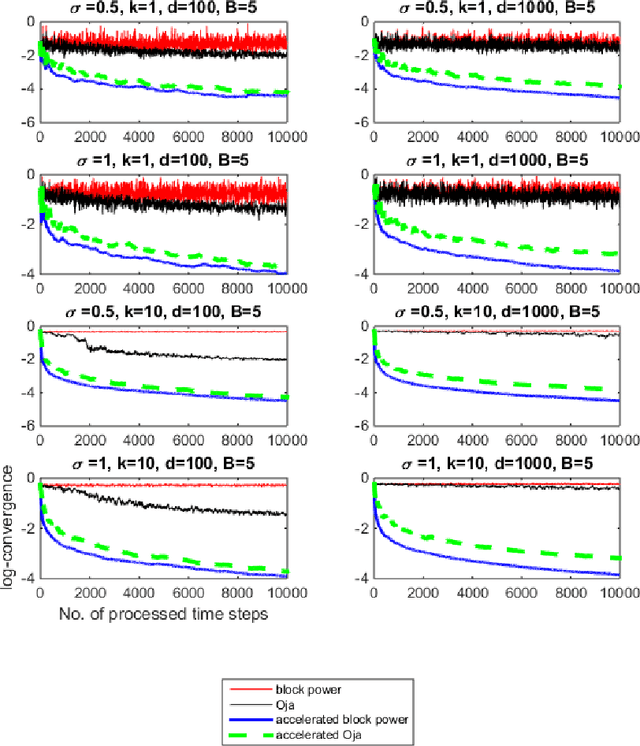
In this paper, we propose an acceleration scheme for online memory-limited PCA methods. Our scheme converges to the first $k>1$ eigenvectors in a single data pass. We provide empirical convergence results of our scheme based on the spiked covariance model. Our scheme does not require any predefined parameters such as the eigengap and hence is well facilitated for streaming data scenarios. Furthermore, we apply our scheme to challenging time-varying systems where online PCA methods fail to converge. Specifically, we discuss a family of time-varying systems that are based on Molecular Dynamics simulations where batch PCA converges to the actual analytic solution of such systems.

Adaptive PCA for Time-Varying Data

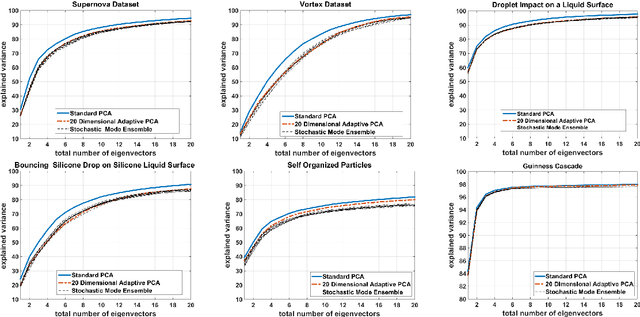
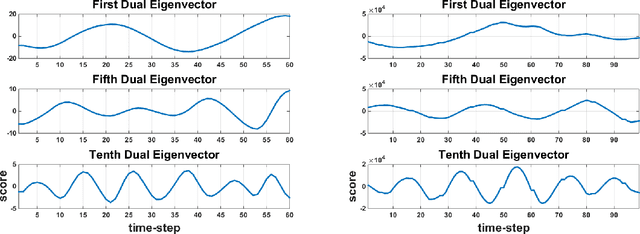
In this paper, we present an online adaptive PCA algorithm that is able to compute the full dimensional eigenspace per new time-step of sequential data. The algorithm is based on a one-step update rule that considers all second order correlations between previous samples and the new time-step. Our algorithm has O(n) complexity per new time-step in its deterministic mode and O(1) complexity per new time-step in its stochastic mode. We test our algorithm on a number of time-varying datasets of different physical phenomena. Explained variance curves indicate that our technique provides an excellent approximation to the original eigenspace computed using standard PCA in batch mode. In addition, our experiments show that the stochastic mode, despite its much lower computational complexity, converges to the same eigenspace computed using the deterministic mode.