F-INR: Functional Tensor Decomposition for Implicit Neural Representations

Implicit Neural Representation (INR) has emerged as a powerful tool for encoding discrete signals into continuous, differentiable functions using neural networks. However, these models often have an unfortunate reliance on monolithic architectures to represent high-dimensional data, leading to prohibitive computational costs as dimensionality grows. We propose F-INR, a framework that reformulates INR learning through functional tensor decomposition, breaking down high-dimensional tasks into lightweight, axis-specific sub-networks. Each sub-network learns a low-dimensional data component (e.g., spatial or temporal). Then, we combine these components via tensor operations, reducing forward pass complexity while improving accuracy through specialized learning. F-INR is modular and, therefore, architecture-agnostic, compatible with MLPs, SIREN, WIRE, or other state-of-the-art INR architecture. It is also decomposition-agnostic, supporting CP, TT, and Tucker modes with user-defined rank for speed-accuracy control. In our experiments, F-INR trains $100\times$ faster than existing approaches on video tasks while achieving higher fidelity (+3.4 dB PSNR). Similar gains hold for image compression, physics simulations, and 3D geometry reconstruction. Through this, F-INR offers a new scalable, flexible solution for high-dimensional signal modeling.

Functional Tensor Decompositions for Physics-Informed Neural Networks

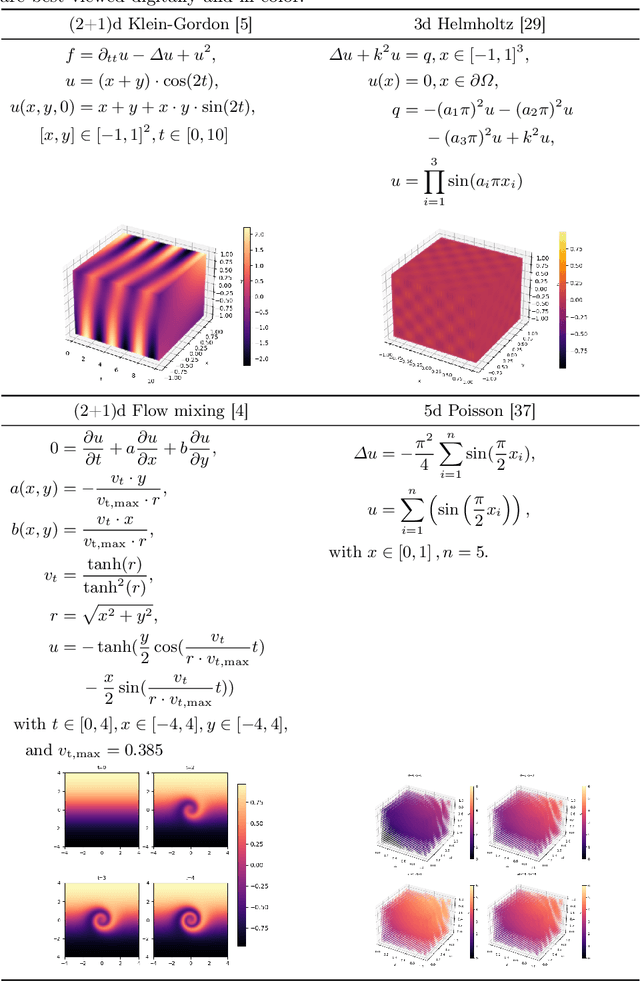
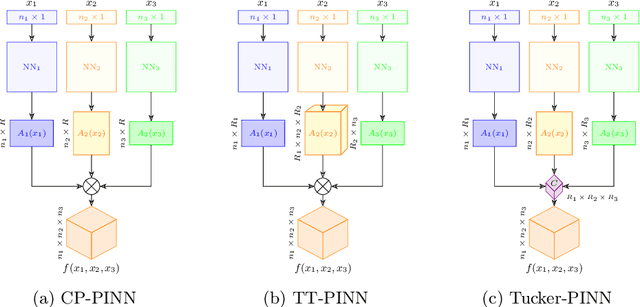
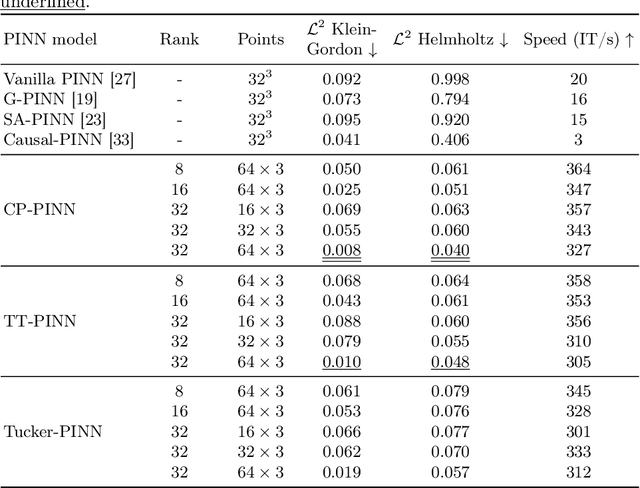
Physics-Informed Neural Networks (PINNs) have shown continuous and increasing promise in approximating partial differential equations (PDEs), although they remain constrained by the curse of dimensionality. In this paper, we propose a generalized PINN version of the classical variable separable method. To do this, we first show that, using the universal approximation theorem, a multivariate function can be approximated by the outer product of neural networks, whose inputs are separated variables. We leverage tensor decomposition forms to separate the variables in a PINN setting. By employing Canonic Polyadic (CP), Tensor-Train (TT), and Tucker decomposition forms within the PINN framework, we create robust architectures for learning multivariate functions from separate neural networks connected by outer products. Our methodology significantly enhances the performance of PINNs, as evidenced by improved results on complex high-dimensional PDEs, including the 3d Helmholtz and 5d Poisson equations, among others. This research underscores the potential of tensor decomposition-based variably separated PINNs to surpass the state-of-the-art, offering a compelling solution to the dimensionality challenge in PDE approximation.