On Chord and Sagitta in ${\mathbb Z}^2$: An Analysis towards Fast and Robust Circular Arc Detection

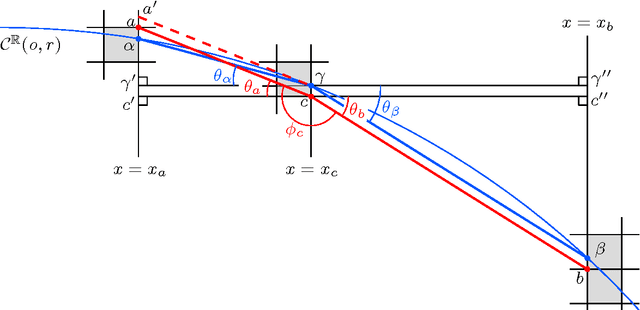
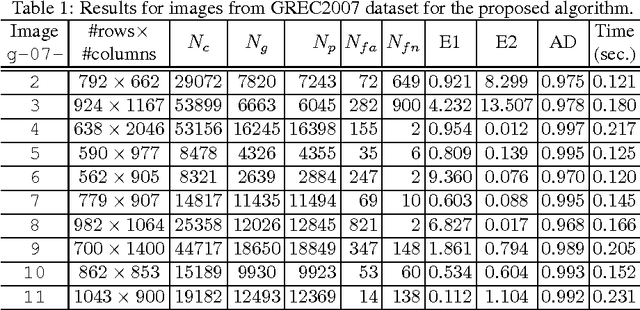
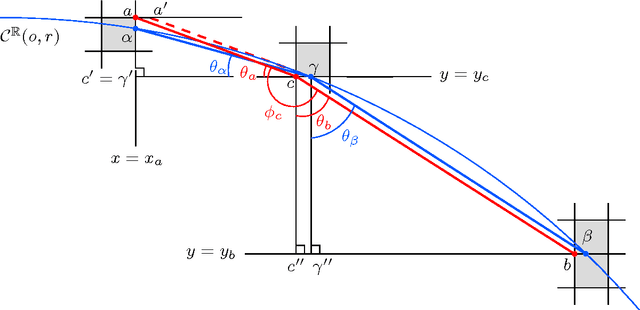
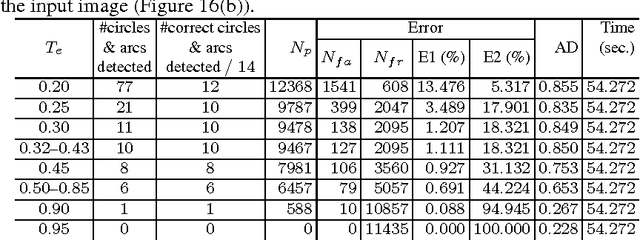
Although chord and sagitta, when considered in tandem, may reflect many underlying geometric properties of circles on the Euclidean plane, their implications on the digital plane are not yet well-understood. In this paper, we explore some of their fundamental properties on the digital plane that have a strong bearing on the unsupervised detection of circles and circular arcs in a digital image. We show that although the chord-and-sagitta properties of a real circle do not readily migrate to the digital plane, they can indeed be used for the analysis in the discrete domain based on certain bounds on their deviations, which are derived from the real domain. In particular, we derive an upper bound on the circumferential angular deviation of a point in the context of chord property, and an upper bound on the relative error in radius estimation with regard to the sagitta property. Using these two bounds, we design a novel algorithm for the detection and parameterization of circles and circular arcs, which does not require any heuristic initialization or manual tuning. The chord property is deployed for the detection of circular arcs, whereas the sagitta property is used to estimate their centers and radii. Finally, to improve the accuracy of estimation, the notion of restricted Hough transform is used. Experimental results demonstrate superior efficiency and robustness of the proposed methodology compared to existing techniques.