A Prufer-Sequence Based Representation of Large Graphs for Structural Encoding of Logic Networks

The pervasiveness of graphs in today's real life systems is quite evident, where the system either explicitly exists as graph or can be readily modelled as one. Such graphical structure is thus a store house rich information. This has various implication depending on whether we are interested in a node or the graph as a whole. In this paper, we are primarily concerned with the later, that is, the inference that the structure of the graph influences the property of the real life system it represents. A model of such structural influence would be useful in inferencing useful properties of complex and large systems, like VLSI circuits, through its structural property. However, before we can apply some machine learning (ML) based technique to model such relationship, an effective representation of the graph is imperative. In this paper, we propose a graph representation which is lossless, linear-sized in terms of number of vertices and gives a 1-D representation of the graph. Our representation is based on Prufer encoding for trees. Moreover, our method is based on a novel technique, called $\mathcal{GT}$-enhancement whereby we first transform the graph such that it can be represented by a singular tree. The encoding also provides scope to include additional graph property and improve the interpretability of the code.

On Chord and Sagitta in ${\mathbb Z}^2$: An Analysis towards Fast and Robust Circular Arc Detection

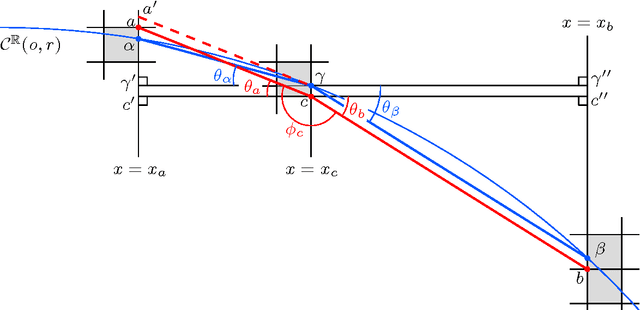
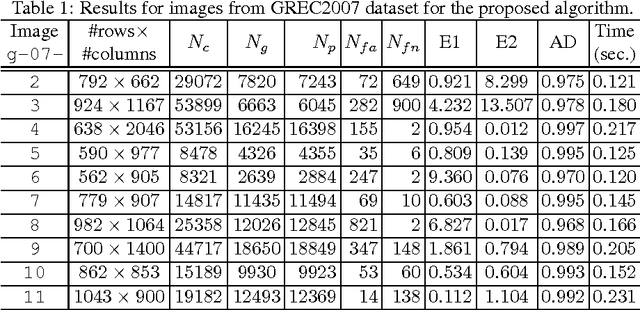
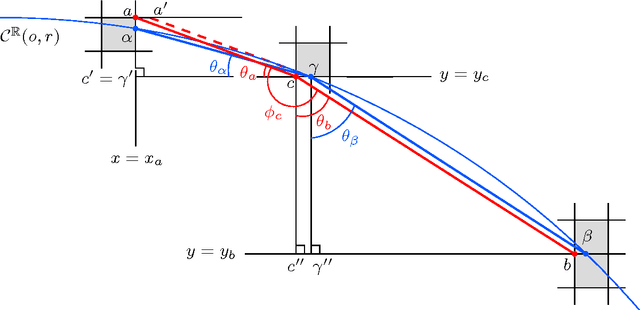
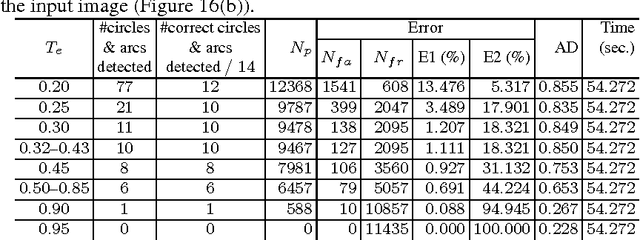
Although chord and sagitta, when considered in tandem, may reflect many underlying geometric properties of circles on the Euclidean plane, their implications on the digital plane are not yet well-understood. In this paper, we explore some of their fundamental properties on the digital plane that have a strong bearing on the unsupervised detection of circles and circular arcs in a digital image. We show that although the chord-and-sagitta properties of a real circle do not readily migrate to the digital plane, they can indeed be used for the analysis in the discrete domain based on certain bounds on their deviations, which are derived from the real domain. In particular, we derive an upper bound on the circumferential angular deviation of a point in the context of chord property, and an upper bound on the relative error in radius estimation with regard to the sagitta property. Using these two bounds, we design a novel algorithm for the detection and parameterization of circles and circular arcs, which does not require any heuristic initialization or manual tuning. The chord property is deployed for the detection of circular arcs, whereas the sagitta property is used to estimate their centers and radii. Finally, to improve the accuracy of estimation, the notion of restricted Hough transform is used. Experimental results demonstrate superior efficiency and robustness of the proposed methodology compared to existing techniques.