Symplectic convolutional neural networks

We propose a new symplectic convolutional neural network (CNN) architecture by leveraging symplectic neural networks, proper symplectic decomposition, and tensor techniques. Specifically, we first introduce a mathematically equivalent form of the convolution layer and then, using symplectic neural networks, we demonstrate a way to parameterize the layers of the CNN to ensure that the convolution layer remains symplectic. To construct a complete autoencoder, we introduce a symplectic pooling layer. We demonstrate the performance of the proposed neural network on three examples: the wave equation, the nonlinear Schr\"odinger (NLS) equation, and the sine-Gordon equation. The numerical results indicate that the symplectic CNN outperforms the linear symplectic autoencoder obtained via proper symplectic decomposition.

Structure-preserving learning for multi-symplectic PDEs

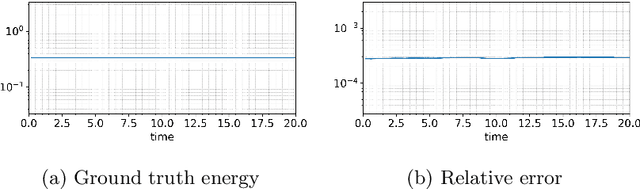
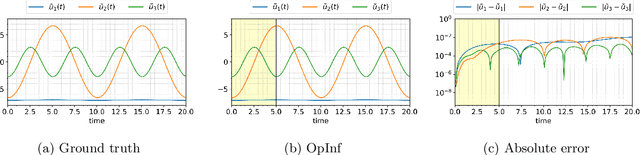
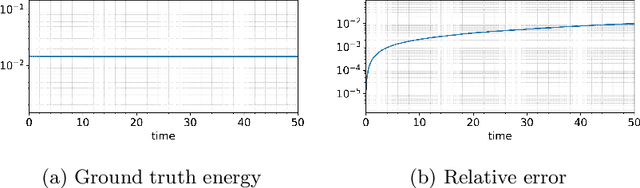
This paper presents an energy-preserving machine learning method for inferring reduced-order models (ROMs) by exploiting the multi-symplectic form of partial differential equations (PDEs). The vast majority of energy-preserving reduced-order methods use symplectic Galerkin projection to construct reduced-order Hamiltonian models by projecting the full models onto a symplectic subspace. However, symplectic projection requires the existence of fully discrete operators, and in many cases, such as black-box PDE solvers, these operators are inaccessible. In this work, we propose an energy-preserving machine learning method that can infer the dynamics of the given PDE using data only, so that the proposed framework does not depend on the fully discrete operators. In this context, the proposed method is non-intrusive. The proposed method is grey box in the sense that it requires only some basic knowledge of the multi-symplectic model at the partial differential equation level. We prove that the proposed method satisfies spatially discrete local energy conservation and preserves the multi-symplectic conservation laws. We test our method on the linear wave equation, the Korteweg-de Vries equation, and the Zakharov-Kuznetsov equation. We test the generalization of our learned models by testing them far outside the training time interval.

Deep Learning for Structure-Preserving Universal Stable Koopman-Inspired Embeddings for Nonlinear Canonical Hamiltonian Dynamics

Discovering a suitable coordinate transformation for nonlinear systems enables the construction of simpler models, facilitating prediction, control, and optimization for complex nonlinear systems. To that end, Koopman operator theory offers a framework for global linearization for nonlinear systems, thereby allowing the usage of linear tools for design studies. In this work, we focus on the identification of global linearized embeddings for canonical nonlinear Hamiltonian systems through a symplectic transformation. While this task is often challenging, we leverage the power of deep learning to discover the desired embeddings. Furthermore, to overcome the shortcomings of Koopman operators for systems with continuous spectra, we apply the lifting principle and learn global cubicized embeddings. Additionally, a key emphasis is paid to enforce the bounded stability for the dynamics of the discovered embeddings. We demonstrate the capabilities of deep learning in acquiring compact symplectic coordinate transformation and the corresponding simple dynamical models, fostering data-driven learning of nonlinear canonical Hamiltonian systems, even those with continuous spectra.