Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Mastering NIM and Impartial Games with Weak Neural Networks: An AlphaZero-inspired Multi-Frame Approach

This paper provides a theoretical framework that validates and explains the results in the work with Bei Zhou experimentally finding that AlphaZero-style reinforcement learning algorithms struggle to learn optimal play in NIM, a canonical impartial game proposed as an AI challenge by Harvey Friedman in 2017. Our analysis resolves a controversy around these experimental results, which revealed unexpected difficulties in learning NIM despite its mathematical simplicity compared to games like chess and Go. Our key contributions are as follows: We prove that by incorporating recent game history, these limited AlphaZero models can, in principle, achieve optimal play in NIM. We introduce a novel search strategy where roll-outs preserve game-theoretic values during move selection, guided by a specialised policy network. We provide constructive proofs showing that our approach enables optimal play within the \(\text{AC}^0\) complexity class despite the theoretical limitations of these networks. This research demonstrates how constrained neural networks when properly designed, can achieve sophisticated decision-making even in domains where their basic computational capabilities appear insufficient.

Impartial Games: A Challenge for Reinforcement Learning

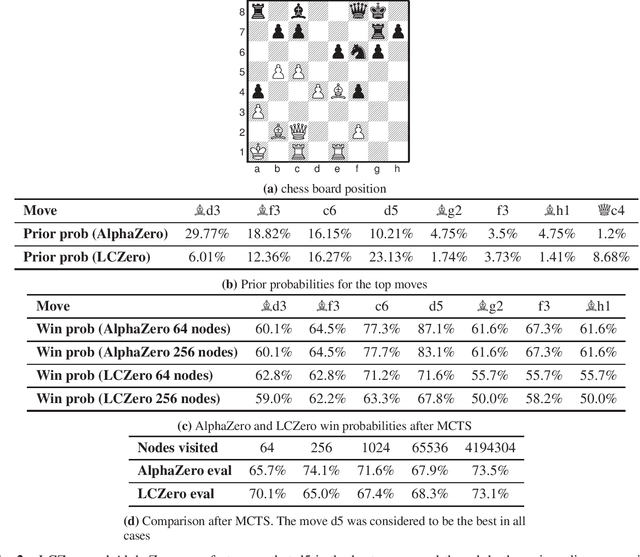
The AlphaZero algorithm and its successor MuZero have revolutionised several competitive strategy games, including chess, Go, and shogi and video games like Atari, by learning to play these games better than any human and any specialised computer program. Aside from knowing the rules, AlphaZero had no prior knowledge of each game. This dramatically advanced progress on a long-standing AI challenge to create programs that can learn for themselves from first principles. Theoretically, there are well-known limits to the power of deep learning for strategy games like chess, Go, and shogi, as they are known to be NEXPTIME hard. Some papers have argued that the AlphaZero methodology has limitations and is unsuitable for general AI. However, none of these works has suggested any specific limits for any particular game. In this paper, we provide more powerful bottlenecks than previously suggested. We present the first concrete example of a game - namely the (children) game of nim - and other impartial games that seem to be a stumbling block for AlphaZero and similar reinforcement learning algorithms. We show experimentally that the bottlenecks apply to both the policy and value networks. Since solving nim can be done in linear time using logarithmic space i.e. has very low-complexity, our experimental results supersede known theoretical limits based on many games' PSPACE (and NEXPTIME) completeness. We show that nim can be learned on small boards, but when the board size increases, AlphaZero style algorithms rapidly fail to improve. We quantify the difficulties for various setups, parameter settings and computational resources. Our results might help expand the AlphaZero self-play paradigm by allowing it to use meta-actions during training and/or actual game play like applying abstract transformations, or reading and writing to an external memory.