Feature subset selection for kernel SVM classification via mixed-integer optimization

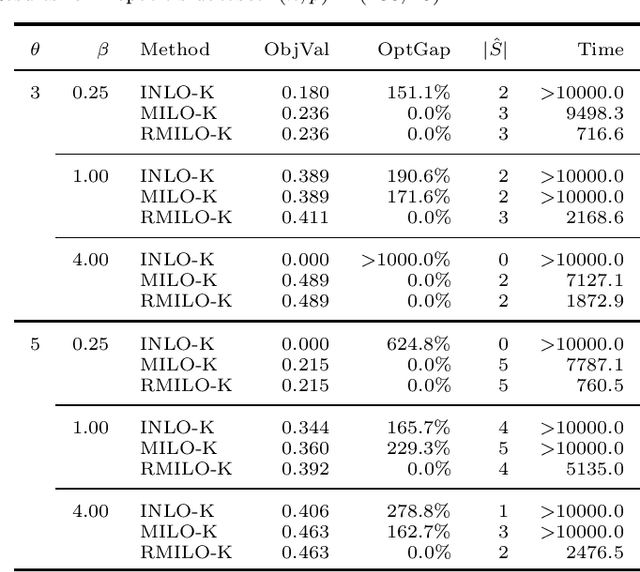
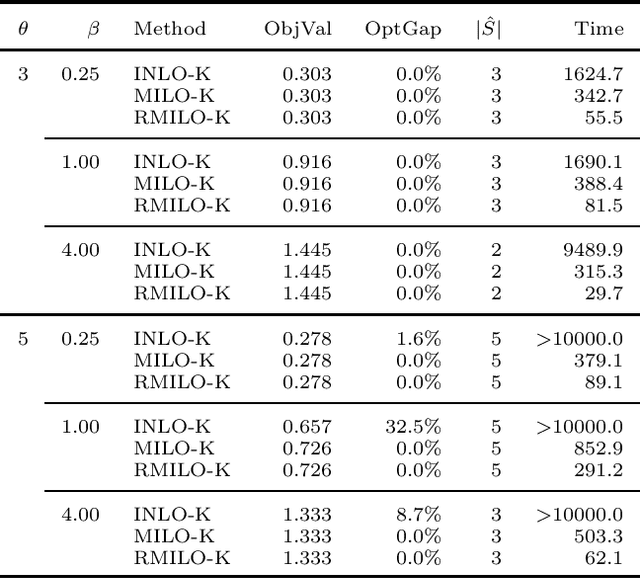
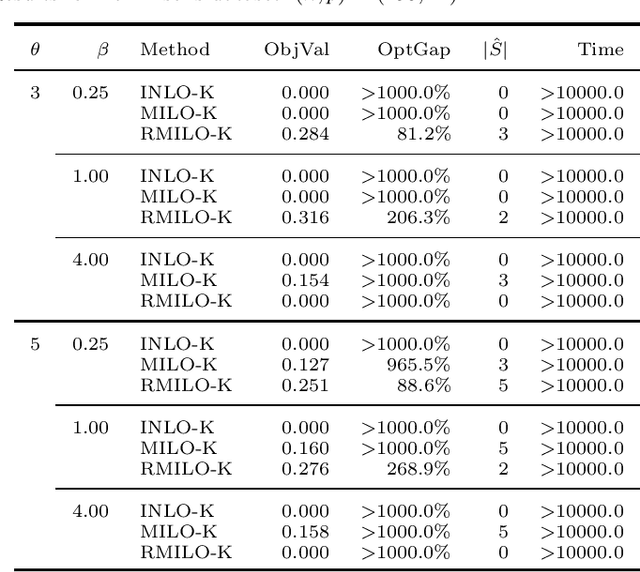
We study the mixed-integer optimization (MIO) approach to feature subset selection in nonlinear kernel support vector machines (SVMs) for binary classification. First proposed for linear regression in the 1970s, this approach has recently moved into the spotlight with advances in optimization algorithms and computer hardware. The goal of this paper is to establish an MIO approach for selecting the best subset of features for kernel SVM classification. To measure the performance of subset selection, we use the kernel-target alignment, which is the distance between the centroids of two response classes in a high-dimensional feature space. We propose a mixed-integer linear optimization (MILO) formulation based on the kernel-target alignment for feature subset selection, and this MILO problem can be solved to optimality using optimization software. We also derive a reduced version of the MILO problem to accelerate our MILO computations. Experimental results show good computational efficiency for our MILO formulation with the reduced problem. Moreover, our method can often outperform the linear-SVM-based MILO formulation and recursive feature elimination in prediction performance, especially when there are relatively few data instances.

Piecewise-Linear Approximation for Feature Subset Selection in a Sequential Logit Model

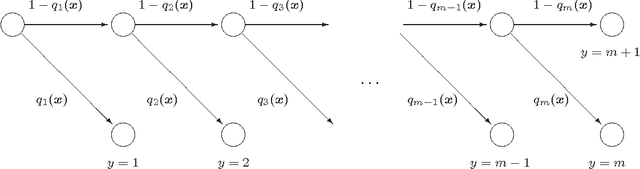
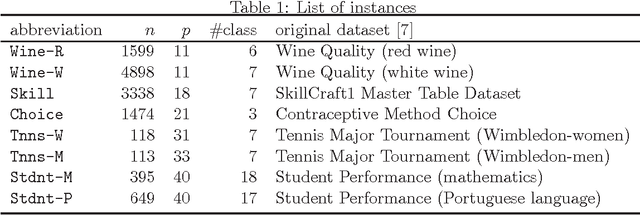
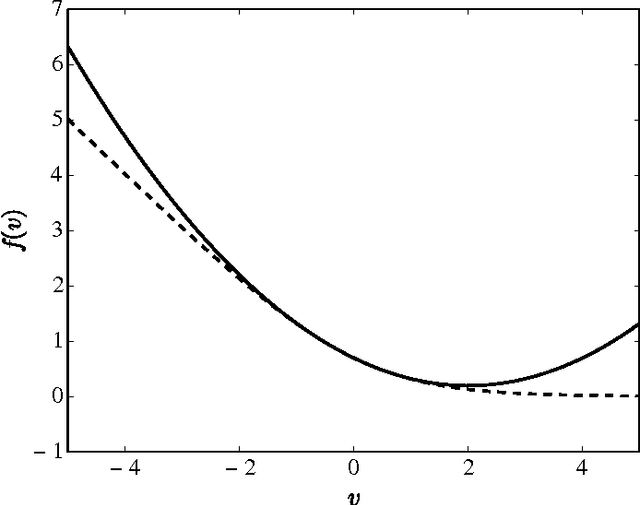
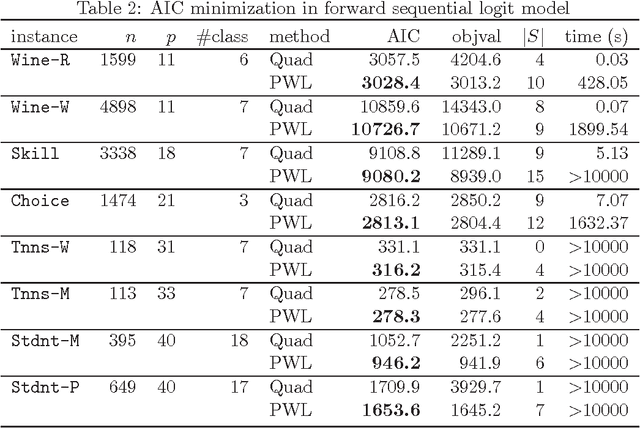
This paper concerns a method of selecting a subset of features for a sequential logit model. Tanaka and Nakagawa (2014) proposed a mixed integer quadratic optimization formulation for solving the problem based on a quadratic approximation of the logistic loss function. However, since there is a significant gap between the logistic loss function and its quadratic approximation, their formulation may fail to find a good subset of features. To overcome this drawback, we apply a piecewise-linear approximation to the logistic loss function. Accordingly, we frame the feature subset selection problem of minimizing an information criterion as a mixed integer linear optimization problem. The computational results demonstrate that our piecewise-linear approximation approach found a better subset of features than the quadratic approximation approach.