Active Learning Classification from a Signal Separation Perspective

In machine learning, classification is usually seen as a function approximation problem, where the goal is to learn a function that maps input features to class labels. In this paper, we propose a novel clustering and classification framework inspired by the principles of signal separation. This approach enables efficient identification of class supports, even in the presence of overlapping distributions. We validate our method on real-world hyperspectral datasets Salinas and Indian Pines. The experimental results demonstrate that our method is competitive with the state of the art active learning algorithms by using a very small subset of data set as training points.

Learning on manifolds without manifold learning

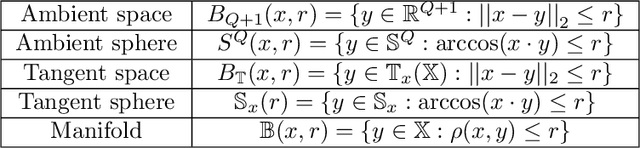
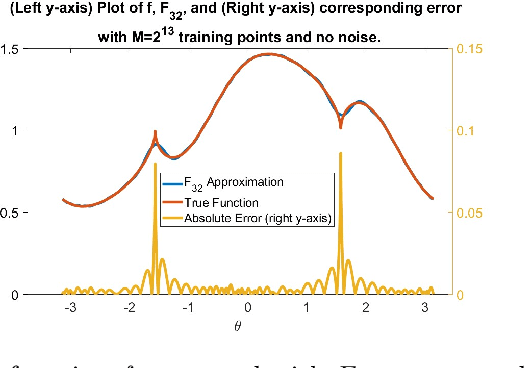
Function approximation based on data drawn randomly from an unknown distribution is an important problem in machine learning. In contrast to the prevalent paradigm of solving this problem by minimizing a loss functional, we have given a direct one-shot construction together with optimal error bounds under the manifold assumption; i.e., one assumes that the data is sampled from an unknown sub-manifold of a high dimensional Euclidean space. A great deal of research deals with obtaining information about this manifold, such as the eigendecomposition of the Laplace-Beltrami operator or coordinate charts, and using this information for function approximation. This two step approach implies some extra errors in the approximation stemming from basic quantities of the data in addition to the errors inherent in function approximation. In Neural Networks, 132:253268, 2020, we have proposed a one-shot direct method to achieve function approximation without requiring the extraction of any information about the manifold other than its dimension. However, one cannot pin down the class of approximants used in that paper. In this paper, we view the unknown manifold as a sub-manifold of an ambient hypersphere and study the question of constructing a one-shot approximation using the spherical polynomials based on the hypersphere. Our approach does not require preprocessing of the data to obtain information about the manifold other than its dimension. We give optimal rates of approximation for relatively "rough" functions.

Local transfer learning from one data space to another

A fundamental problem in manifold learning is to approximate a functional relationship in a data chosen randomly from a probability distribution supported on a low dimensional sub-manifold of a high dimensional ambient Euclidean space. The manifold is essentially defined by the data set itself and, typically, designed so that the data is dense on the manifold in some sense. The notion of a data space is an abstraction of a manifold encapsulating the essential properties that allow for function approximation. The problem of transfer learning (meta-learning) is to use the learning of a function on one data set to learn a similar function on a new data set. In terms of function approximation, this means lifting a function on one data space (the base data space) to another (the target data space). This viewpoint enables us to connect some inverse problems in applied mathematics (such as inverse Radon transform) with transfer learning. In this paper we examine the question of such lifting when the data is assumed to be known only on a part of the base data space. We are interested in determining subsets of the target data space on which the lifting can be defined, and how the local smoothness of the function and its lifting are related.