Twin Sorting Dynamic Programming Assisted User Association and Wireless Bandwidth Allocation for Hierarchical Federated Learning

In this paper, we study user association and wireless bandwidth allocation for a hierarchical federated learning system that consists of mobile users, edge servers, and a cloud server. To minimize the length of a global round in hierarchical federated learning with equal bandwidth allocation, we formulate a combinatorial optimization problem. We design the twin sorting dynamic programming (TSDP) algorithm that obtains a globally optimal solution in polynomial time when there are two edge servers. In addition, we put forward the TSDP-assisted algorithm for user association when there are three or more edge servers. Furthermore, given a user association matrix, we formulate and solve a convex optimization problem for optimal wireless bandwidth allocation. Simulation results show that the proposed approach outperforms a number of alternative schemes.

Greedier is Better: Selecting Multiple Neighbors per Iteration for Sparse Subspace Clustering

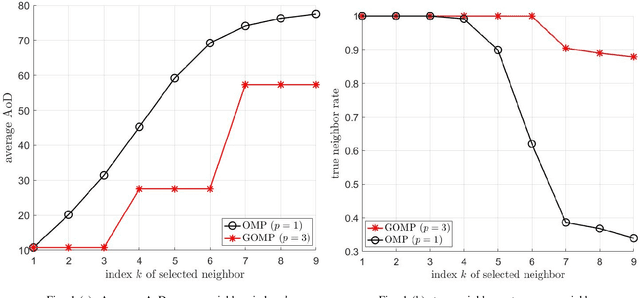
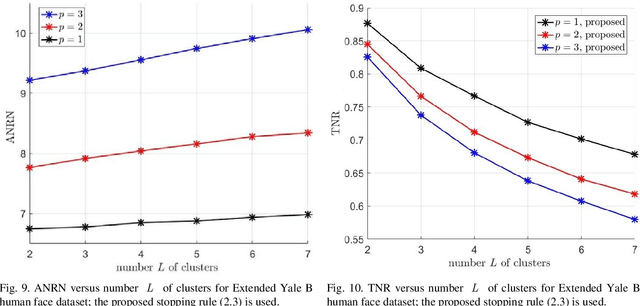
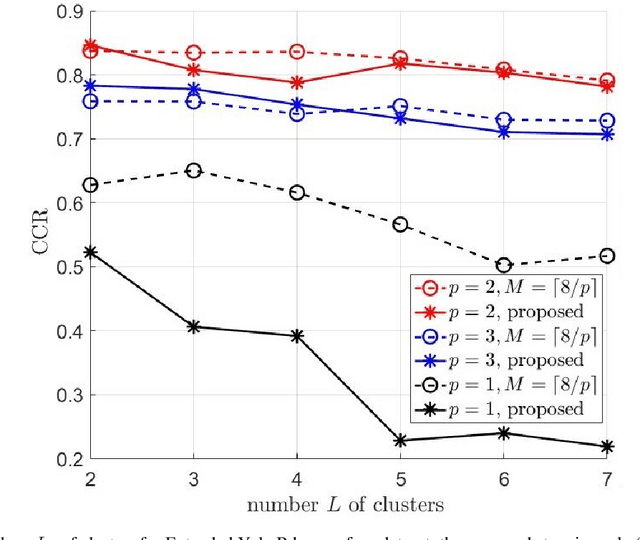
Sparse subspace clustering (SSC) using greedy-based neighbor selection, such as orthogonal matching pursuit (OMP), has been known as a popular computationally-efficient alternative to the popular L1-minimization based methods. This paper proposes a new SSC scheme using generalized OMP (GOMP), a soup-up of OMP whereby multiple neighbors are identified per iteration, along with a new stopping rule requiring nothing more than a knowledge of the ambient signal dimension. Compared to conventional OMP, which identifies one neighbor per iteration, the proposed GOMP method involves fewer iterations, thereby enjoying lower algorithmic complexity; advantageously, the proposed stopping rule is free from off-line estimation of subspace dimension and noise power. Under the semi-random model, analytic performance guarantees, in terms of neighbor recovery rates, are established to justify the advantage of the proposed GOMP. The results show that, with a high probability, GOMP (i) is halted by the proposed stopping rule, and (ii) can retrieve more true neighbors than OMP, consequently yielding higher final data clustering accuracy. Computer simulations using both synthetic data and real human face data are provided to validate our analytic study and evidence the effectiveness of the proposed approach.

Federated Learning Over Cellular-Connected UAV Networks with Non-IID Datasets

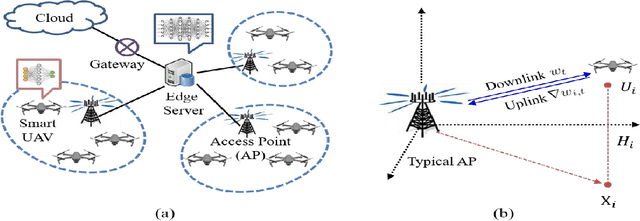
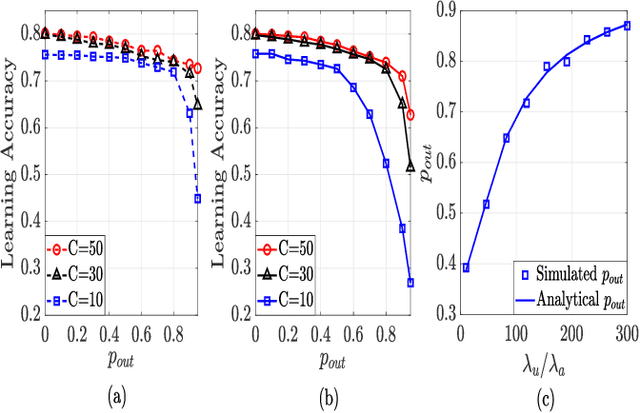
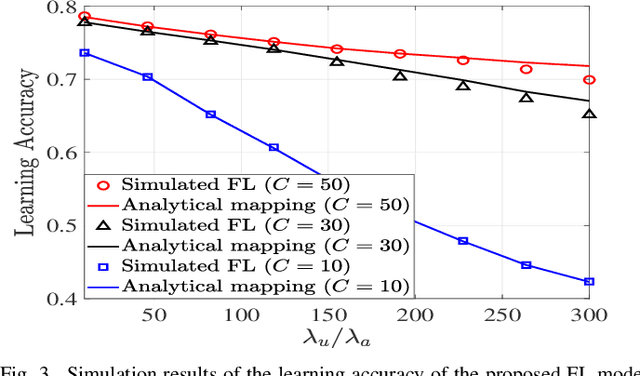
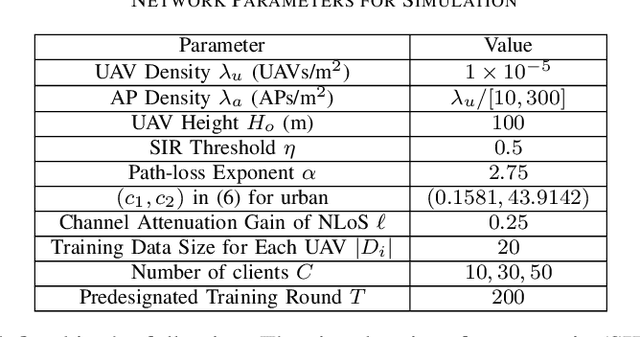
Federated learning (FL) is a promising distributed learning technique particularly suitable for wireless learning scenarios since it can accomplish a learning task without raw data transportation so as to preserve data privacy and lower network resource consumption. However, current works on FL over wireless communication do not profoundly study the fundamental performance of FL that suffers from data delivery outage due to network interference and data heterogeneity among mobile clients. To accurately exploit the performance of FL over wireless communication, this paper proposes a new FL model over a cellular-connected unmanned aerial vehicle (UAV) network, which characterizes data delivery outage from UAV clients to their server and data heterogeneity among the datasets of UAV clients. We devise a simulation-based approach to evaluating the convergence performance of the proposed FL model. We then propose a tractable analytical framework of the uplink outage probability in the cellular-connected UAV network and derive a neat expression of the uplink outage probability, which reveals how the proposed FL model is impacted by data delivery outage and UAV deployment. Extensive numerical simulations are conducted to show the consistency between the estimated and simulated performances.

Provable Noisy Sparse Subspace Clustering using Greedy Neighbor Selection: A Coherence-Based Perspective

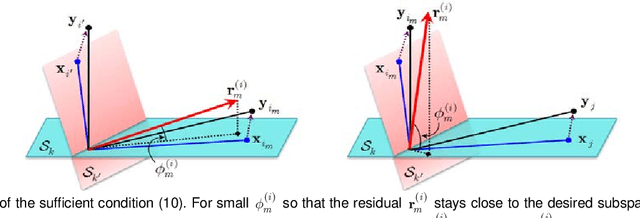
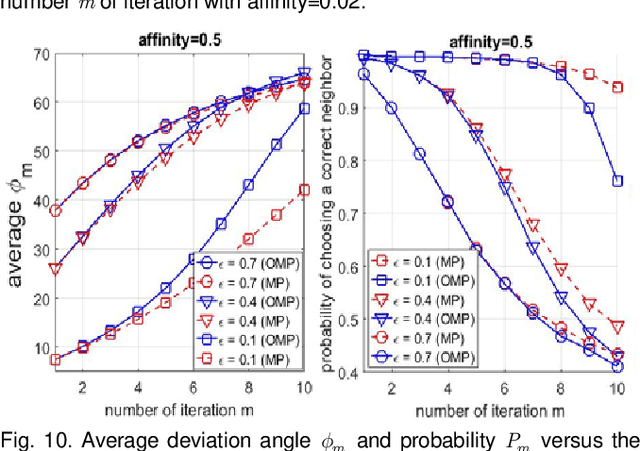
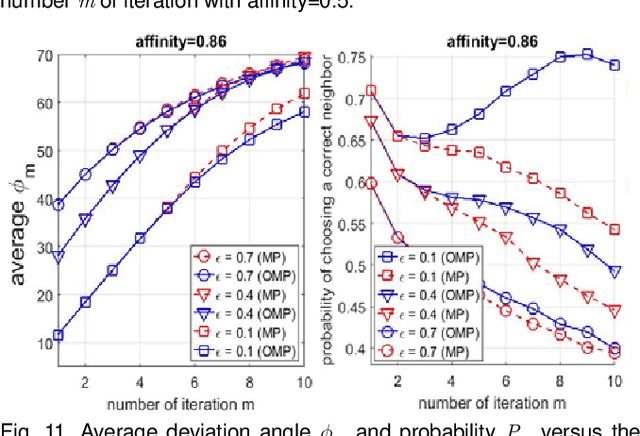
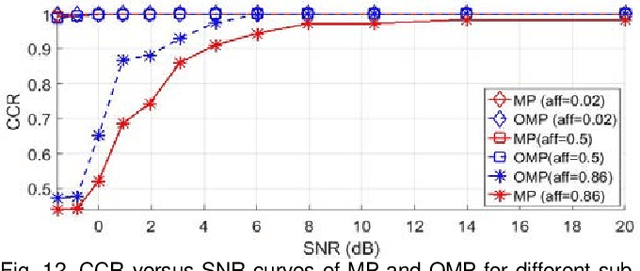
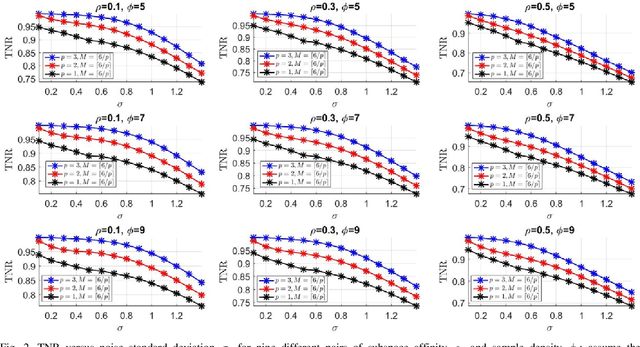
Sparse subspace clustering (SSC) using greedy-based neighbor selection, such as matching pursuit (MP) and orthogonal matching pursuit (OMP), has been known as a popular computationally-efficient alternative to the conventional L1-minimization based methods. Under deterministic bounded noise corruption, in this paper we derive coherence-based sufficient conditions guaranteeing correct neighbor identification using MP/OMP. Our analyses exploit the maximum/minimum inner product between two noisy data points subject to a known upper bound on the noise level. The obtained sufficient condition clearly reveals the impact of noise on greedy-based neighbor recovery. Specifically, it asserts that, as long as noise is sufficiently small so that the resultant perturbed residual vectors stay close to the desired subspace, both MP and OMP succeed in returning a correct neighbor subset. A striking finding is that, when the ground truth subspaces are well-separated from each other and noise is not large, MP-based iterations, while enjoying lower algorithmic complexity, yield smaller perturbation of residuals, thereby better able to identify correct neighbors and, in turn, achieving higher global data clustering accuracy. Extensive numerical experiments are used to corroborate our theoretical study.