Liang-Chi Huang
A Metric Topology of Deep Learning for Data Classification
Jan 20, 2025
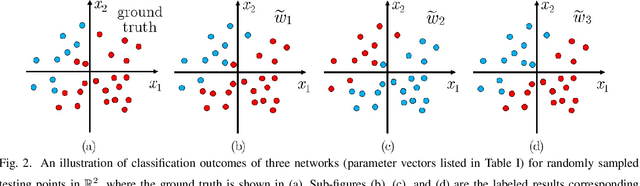
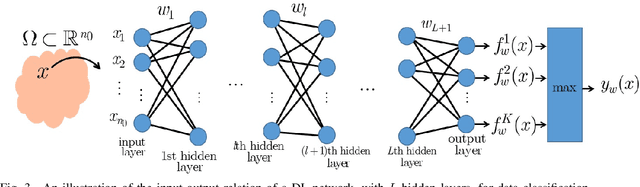
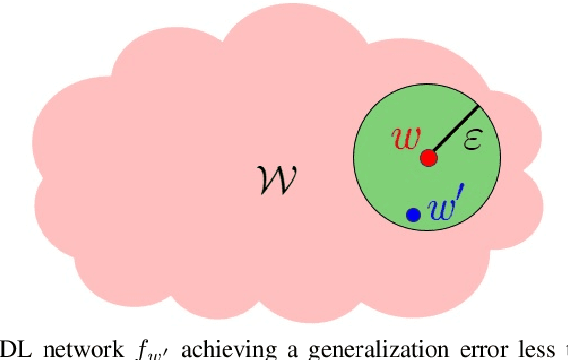
Abstract:Empirically, Deep Learning (DL) has demonstrated unprecedented success in practical applications. However, DL remains by and large a mysterious "black-box", spurring recent theoretical research to build its mathematical foundations. In this paper, we investigate DL for data classification through the prism of metric topology. Considering that conventional Euclidean metric over the network parameter space typically fails to discriminate DL networks according to their classification outcomes, we propose from a probabilistic point of view a meaningful distance measure, whereby DL networks yielding similar classification performances are close. The proposed distance measure defines such an equivalent relation among network parameter vectors that networks performing equally well belong to the same equivalent class. Interestingly, our proposed distance measure can provably serve as a metric on the quotient set modulo the equivalent relation. Then, under quite mild conditions it is shown that, apart from a vanishingly small subset of networks likely to predict non-unique labels, our proposed metric space is compact, and coincides with the well-known quotient topological space. Our study contributes to fundamental understanding of DL, and opens up new ways of studying DL using fruitful metric space theory.
Greedier is Better: Selecting Multiple Neighbors per Iteration for Sparse Subspace Clustering
Apr 06, 2022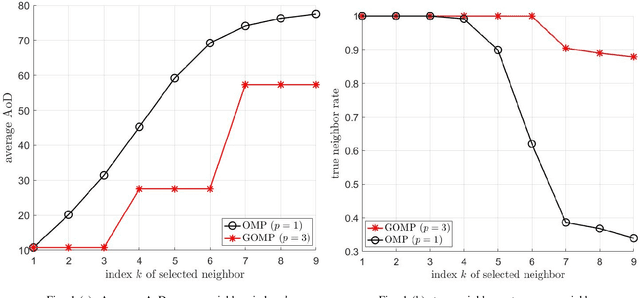
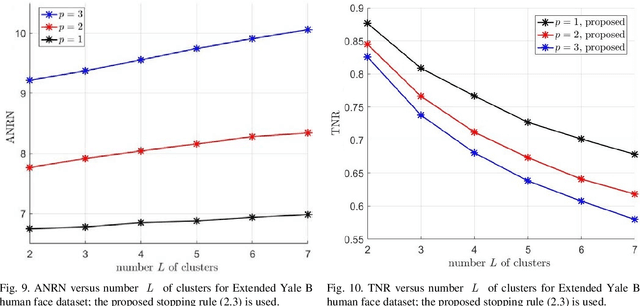
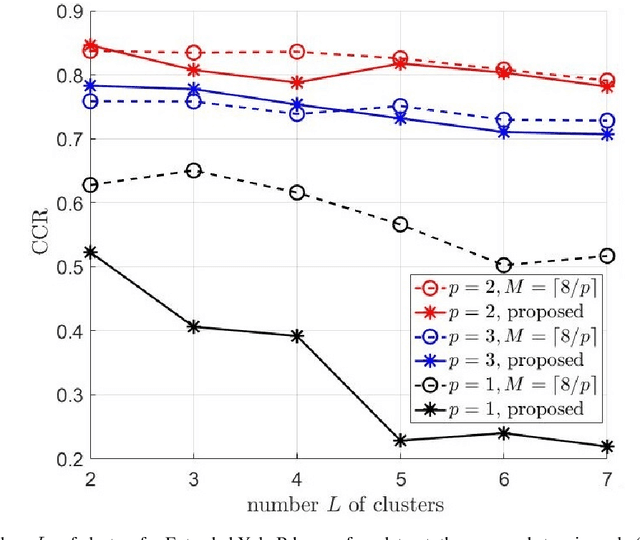
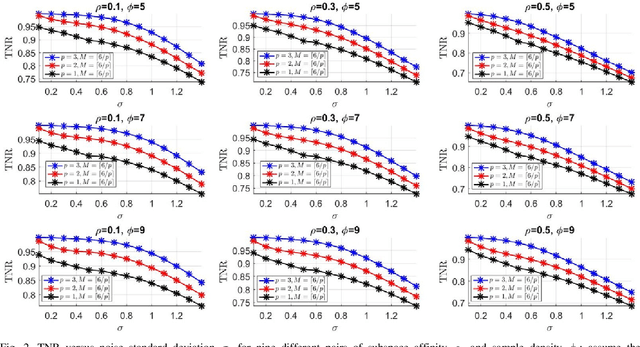
Abstract:Sparse subspace clustering (SSC) using greedy-based neighbor selection, such as orthogonal matching pursuit (OMP), has been known as a popular computationally-efficient alternative to the popular L1-minimization based methods. This paper proposes a new SSC scheme using generalized OMP (GOMP), a soup-up of OMP whereby multiple neighbors are identified per iteration, along with a new stopping rule requiring nothing more than a knowledge of the ambient signal dimension. Compared to conventional OMP, which identifies one neighbor per iteration, the proposed GOMP method involves fewer iterations, thereby enjoying lower algorithmic complexity; advantageously, the proposed stopping rule is free from off-line estimation of subspace dimension and noise power. Under the semi-random model, analytic performance guarantees, in terms of neighbor recovery rates, are established to justify the advantage of the proposed GOMP. The results show that, with a high probability, GOMP (i) is halted by the proposed stopping rule, and (ii) can retrieve more true neighbors than OMP, consequently yielding higher final data clustering accuracy. Computer simulations using both synthetic data and real human face data are provided to validate our analytic study and evidence the effectiveness of the proposed approach.
Provable Noisy Sparse Subspace Clustering using Greedy Neighbor Selection: A Coherence-Based Perspective
Feb 02, 2020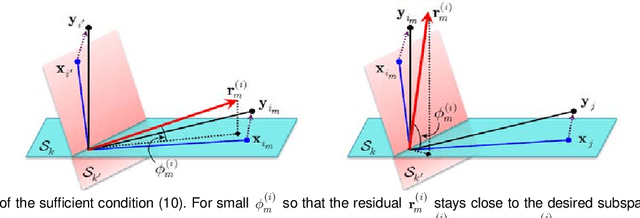
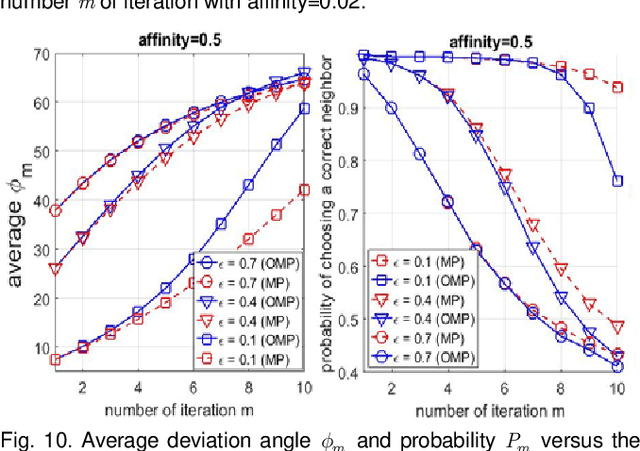
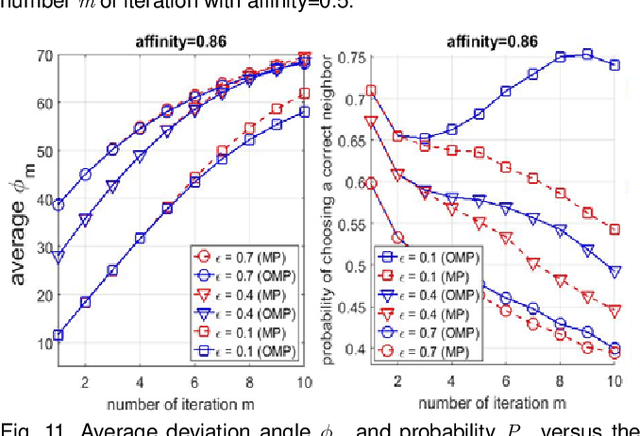
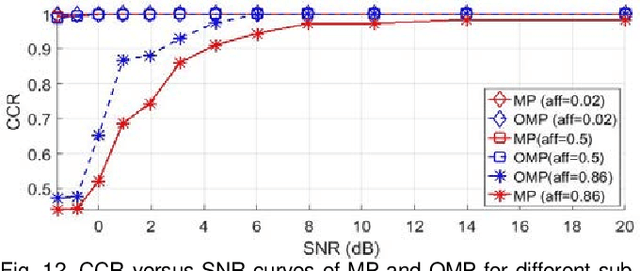
Abstract:Sparse subspace clustering (SSC) using greedy-based neighbor selection, such as matching pursuit (MP) and orthogonal matching pursuit (OMP), has been known as a popular computationally-efficient alternative to the conventional L1-minimization based methods. Under deterministic bounded noise corruption, in this paper we derive coherence-based sufficient conditions guaranteeing correct neighbor identification using MP/OMP. Our analyses exploit the maximum/minimum inner product between two noisy data points subject to a known upper bound on the noise level. The obtained sufficient condition clearly reveals the impact of noise on greedy-based neighbor recovery. Specifically, it asserts that, as long as noise is sufficiently small so that the resultant perturbed residual vectors stay close to the desired subspace, both MP and OMP succeed in returning a correct neighbor subset. A striking finding is that, when the ground truth subspaces are well-separated from each other and noise is not large, MP-based iterations, while enjoying lower algorithmic complexity, yield smaller perturbation of residuals, thereby better able to identify correct neighbors and, in turn, achieving higher global data clustering accuracy. Extensive numerical experiments are used to corroborate our theoretical study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge