Automating the Discovery of Partial Differential Equations in Dynamical Systems

Identifying partial differential equations (PDEs) from data is crucial for understanding the governing mechanisms of natural phenomena, yet it remains a challenging task. We present an extension to the ARGOS framework, ARGOS-RAL, which leverages sparse regression with the recurrent adaptive lasso to identify PDEs from limited prior knowledge automatically. Our method automates calculating partial derivatives, constructing a candidate library, and estimating a sparse model. We rigorously evaluate the performance of ARGOS-RAL in identifying canonical PDEs under various noise levels and sample sizes, demonstrating its robustness in handling noisy and non-uniformly distributed data. We also test the algorithm's performance on datasets consisting solely of random noise to simulate scenarios with severely compromised data quality. Our results show that ARGOS-RAL effectively and reliably identifies the underlying PDEs from data, outperforming the sequential threshold ridge regression method in most cases. We highlight the potential of combining statistical methods, machine learning, and dynamical systems theory to automatically discover governing equations from collected data, streamlining the scientific modeling process.

Automatically identifying ordinary differential equations from data

Discovering nonlinear differential equations that describe system dynamics from empirical data is a fundamental challenge in contemporary science. Here, we propose a methodology to identify dynamical laws by integrating denoising techniques to smooth the signal, sparse regression to identify the relevant parameters, and bootstrap confidence intervals to quantify the uncertainty of the estimates. We evaluate our method on well-known ordinary differential equations with an ensemble of random initial conditions, time series of increasing length, and varying signal-to-noise ratios. Our algorithm consistently identifies three-dimensional systems, given moderately-sized time series and high levels of signal quality relative to background noise. By accurately discovering dynamical systems automatically, our methodology has the potential to impact the understanding of complex systems, especially in fields where data are abundant, but developing mathematical models demands considerable effort.

Explaining the distribution of energy consumption at slow charging infrastructure for electric vehicles from socio-economic data

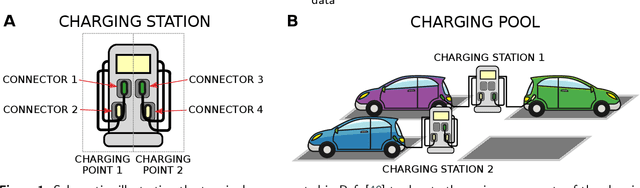
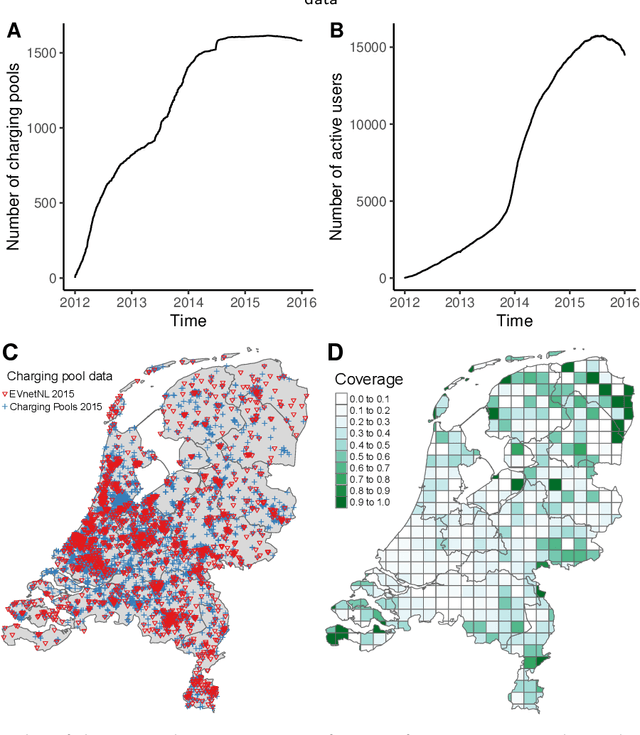
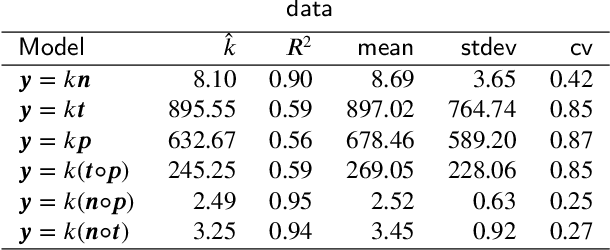
Here, we develop a data-centric approach enabling to analyse which activities, function, and characteristics of the environment surrounding the slow charging infrastructure impact the distribution of the electricity consumed at slow charging infrastructure. To gain a basic insight, we analysed the probabilistic distribution of energy consumption and its relation to indicators characterizing charging events. We collected geospatial datasets and utilizing statistical methods for data pre-processing, we prepared features modelling the spatial context in which the charging infrastructure operates. To enhance the statistical reliability of results, we applied the bootstrap method together with the Lasso method that combines regression with variable selection ability. We evaluate the statistical distributions of the selected regression coefficients. We identified the most influential features correlated with energy consumption, indicating that the spatial context of the charging infrastructure affects its utilization pattern. Many of these features are related to the economic prosperity of residents. Application of the methodology to a specific class of charging infrastructure enables the differentiation of selected features, e.g. by the used rollout strategy. Overall, the paper demonstrates the application of statistical methodologies to energy data and provides insights on factors potentially shaping the energy consumption that could be utilized when developing models to inform charging infrastructure deployment and planning of power grids.

A rigorous definition of axial lines: ridges on isovist fields

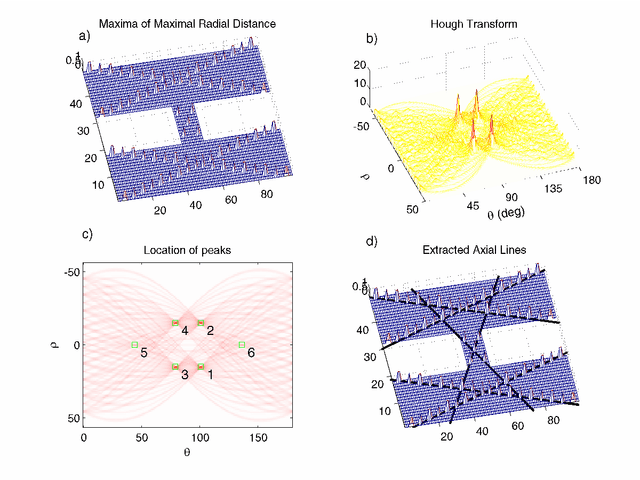
We suggest that 'axial lines' defined by (Hillier and Hanson, 1984) as lines of uninterrupted movement within urban streetscapes or buildings, appear as ridges in isovist fields (Benedikt, 1979). These are formed from the maximum diametric lengths of the individual isovists, sometimes called viewsheds, that make up these fields (Batty and Rana, 2004). We present an image processing technique for the identification of lines from ridges, discuss current strengths and weaknesses of the method, and show how it can be implemented easily and effectively.