Ron van der Meyden
University of New South Wales
Signature in Counterparts, a Formal Treatment
Feb 23, 2020Abstract:"Signature in counterparts" is a legal process that permits a contract between two or more parties to be brought into force by having the parties independently (possibly, remotely) sign different copies of the contract, rather than placing their signatures on a common copy at a physical meeting. The paper develops a logical understanding of this process, developing a number of axioms that can be used to justify the validity of a contract from the assumption that separate copies have been signed. It is argued that a satisfactory account benefits from a logic with syntactic self-reference. The axioms used are supported by a formal semantics, and a number of further properties of this semantics are investigated. In particular, it is shown that the semantics implies that when a contract is valid, the parties do not just agree, but are in mutual agreement (a common-knowledge-like notion) about the validity of the contract.
An Epistemic Foundation for Authentication Logics (Extended Abstract)
Jul 27, 2017
Abstract:While there have been many attempts, going back to BAN logic, to base reasoning about security protocols on epistemic notions, they have not been all that successful. Arguably, this has been due to the particular logics chosen. We present a simple logic based on the well-understood modal operators of knowledge, time, and probability, and show that it is able to handle issues that have often been swept under the rug by other approaches, while being flexible enough to capture all the higher- level security notions that appear in BAN logic. Moreover, while still assuming that the knowledge operator allows for unbounded computation, it can handle the fact that a computationally bounded agent cannot decrypt messages in a natural way, by distinguishing strings and message terms. We demonstrate that our logic can capture BAN logic notions by providing a translation of the BAN operators into our logic, capturing belief by a form of probabilistic knowledge.
* In Proceedings TARK 2017, arXiv:1707.08250
Complete Axiomatizations for Reasoning About Knowledge and Time
Aug 20, 2002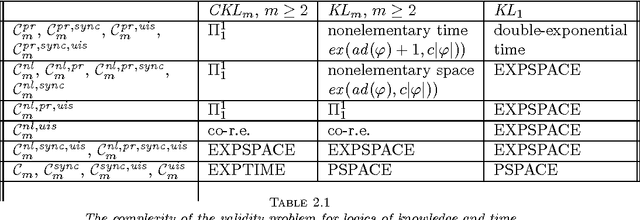
Abstract:Sound and complete axiomatizations are provided for a number of different logics involving modalities for knowledge and time. These logics arise from different choices for various parameters. All the logics considered involve the discrete time linear temporal logic operators `next' and `until' and an operator for the knowledge of each of a number of agents. Both the single agent and multiple agent cases are studied: in some instances of the latter there is also an operator for the common knowledge of the group of all agents. Four different semantic properties of agents are considered: whether they have a unique initial state, whether they operate synchronously, whether they have perfect recall, and whether they learn. The property of no learning is essentially dual to perfect recall. Not all settings of these parameters lead to recursively axiomatizable logics, but sound and complete axiomatizations are presented for all the ones that do.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge