Riccardo Pucella
Forrester Research
An Epistemic Foundation for Authentication Logics (Extended Abstract)
Jul 27, 2017
Abstract:While there have been many attempts, going back to BAN logic, to base reasoning about security protocols on epistemic notions, they have not been all that successful. Arguably, this has been due to the particular logics chosen. We present a simple logic based on the well-understood modal operators of knowledge, time, and probability, and show that it is able to handle issues that have often been swept under the rug by other approaches, while being flexible enough to capture all the higher- level security notions that appear in BAN logic. Moreover, while still assuming that the knowledge operator allows for unbounded computation, it can handle the fact that a computationally bounded agent cannot decrypt messages in a natural way, by distinguishing strings and message terms. We demonstrate that our logic can capture BAN logic notions by providing a translation of the BAN operators into our logic, capturing belief by a form of probabilistic knowledge.
* In Proceedings TARK 2017, arXiv:1707.08250
A Logic for Reasoning about Upper Probabilities
Aug 07, 2014Abstract:We present a propositional logic to reason about the uncertainty of events, where the uncertainty is modeled by a set of probability measures assigning an interval of probability to each event. We give a sound and complete axiomatization for the logic, and show that the satisfiability problem is NP-complete, no harder than satisfiability for propositional logic.
Evidence with Uncertain Likelihoods
Jul 27, 2014Abstract:An agent often has a number of hypotheses, and must choose among them based on observations, or outcomes of experiments. Each of these observations can be viewed as providing evidence for or against various hypotheses. All the attempts to formalize this intuition up to now have assumed that associated with each hypothesis h there is a likelihood function {\mu}h, which is a probability measure that intuitively describes how likely each observation is, conditional on h being the correct hypothesis. We consider an extension of this framework where there is uncertainty as to which of a number of likelihood functions is appropriate, and discuss how one formal approach to defining evidence, which views evidence as a function from priors to posteriors, can be generalized to accommodate this uncertainty.
A Logic for Reasoning about Evidence
Jul 27, 2014Abstract:We introduce a logic for reasoning about evidence, that essentially views evidence as a function from prior beliefs (before making an observation) to posterior beliefs (after making the observation). We provide a sound and complete axiomatization for the logic, and consider the complexity of the decision problem. Although the reasoning in the logic is mainly propositional, we allow variables representing numbers and quantification over them. This expressive power seems necessary to capture important properties of evidence
Reasoning about Expectation
Jul 27, 2014
Abstract:Expectation is a central notion in probability theory. The notion of expectation also makes sense for other notions of uncertainty. We introduce a propositional logic for reasoning about expectation, where the semantics depends on the underlying representation of uncertainty. We give sound and complete axiomatizations for the logic in the case that the underlying representation is (a) probability, (b) sets of probability measures, (c) belief functions, and (d) possibility measures. We show that this logic is more expressive than the corresponding logic for reasoning about likelihood in the case of sets of probability measures, but equi-expressive in the case of probability, belief, and possibility. Finally, we show that satisfiability for these logics is NP-complete, no harder than satisfiability for propositional logic.
Characterizing and Reasoning about Probabilistic and Non-Probabilistic Expectation
Apr 20, 2007
Abstract:Expectation is a central notion in probability theory. The notion of expectation also makes sense for other notions of uncertainty. We introduce a propositional logic for reasoning about expectation, where the semantics depends on the underlying representation of uncertainty. We give sound and complete axiomatizations for the logic in the case that the underlying representation is (a) probability, (b) sets of probability measures, (c) belief functions, and (d) possibility measures. We show that this logic is more expressive than the corresponding logic for reasoning about likelihood in the case of sets of probability measures, but equi-expressive in the case of probability, belief, and possibility. Finally, we show that satisfiability for these logics is NP-complete, no harder than satisfiability for propositional logic.
Dealing With Logical Omniscience: Expressiveness and Pragmatics
Feb 01, 2007Abstract:We examine four approaches for dealing with the logical omniscience problem and their potential applicability: the syntactic approach, awareness, algorithmic knowledge, and impossible possible worlds. Although in some settings these approaches are equi-expressive and can capture all epistemic states, in other settings of interest (especially with probability in the picture), we show that they are not equi-expressive. We then consider the pragmatics of dealing with logical omniscience-- how to choose an approach and construct an appropriate model.
Deductive Algorithmic Knowledge
Jan 18, 2006Abstract:The framework of algorithmic knowledge assumes that agents use algorithms to compute the facts they explicitly know. In many cases of interest, a deductive system, rather than a particular algorithm, captures the formal reasoning used by the agents to compute what they explicitly know. We introduce a logic for reasoning about both implicit and explicit knowledge with the latter defined with respect to a deductive system formalizing a logical theory for agents. The highly structured nature of deductive systems leads to very natural axiomatizations of the resulting logic when interpreted over any fixed deductive system. The decision problem for the logic, in the presence of a single agent, is NP-complete in general, no harder than propositional logic. It remains NP-complete when we fix a deductive system that is decidable in nondeterministic polynomial time. These results extend in a straightforward way to multiple agents.
* 28 pages. A preliminary version of this paper appeared in the Proceedings of the 8th International Symposium on Artificial Intelligence and Mathematics, AI&M 22-2004, 2004
Probabilistic Algorithmic Knowledge
Dec 20, 2005Abstract:The framework of algorithmic knowledge assumes that agents use deterministic knowledge algorithms to compute the facts they explicitly know. We extend the framework to allow for randomized knowledge algorithms. We then characterize the information provided by a randomized knowledge algorithm when its answers have some probability of being incorrect. We formalize this information in terms of evidence; a randomized knowledge algorithm returning ``Yes'' to a query about a fact \phi provides evidence for \phi being true. Finally, we discuss the extent to which this evidence can be used as a basis for decisions.
* 26 pages. A preliminary version appeared in Proc. 9th Conference on Theoretical Aspects of Rationality and Knowledge (TARK'03)
A Framework for Creating Natural Language User Interfaces for Action-Based Applications
Dec 17, 2004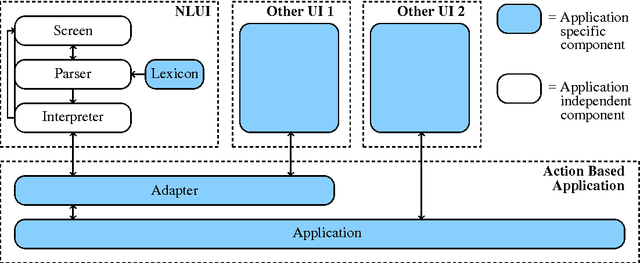
Abstract:In this paper we present a framework for creating natural language interfaces to action-based applications. Our framework uses a number of reusable application-independent components, in order to reduce the effort of creating a natural language interface for a given application. Using a type-logical grammar, we first translate natural language sentences into expressions in an extended higher-order logic. These expressions can be seen as executable specifications corresponding to the original sentences. The executable specifications are then interpreted by invoking appropriate procedures provided by the application for which a natural language interface is being created.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge