On the Role of Memory in Robust Opinion Dynamics

We investigate opinion dynamics in a fully-connected system, consisting of $n$ identical and anonymous agents, where one of the opinions (which is called correct) represents a piece of information to disseminate. In more detail, one source agent initially holds the correct opinion and remains with this opinion throughout the execution. The goal for non-source agents is to quickly agree on this correct opinion, and do that robustly, i.e., from any initial configuration. The system evolves in rounds. In each round, one agent chosen uniformly at random is activated: unless it is the source, the agent pulls the opinions of $\ell$ random agents and then updates its opinion according to some rule. We consider a restricted setting, in which agents have no memory and they only revise their opinions on the basis of those of the agents they currently sample. As restricted as it is, this setting encompasses very popular opinion dynamics, such as the voter model and best-of-$k$ majority rules. Qualitatively speaking, we show that lack of memory prevents efficient convergence. Specifically, we prove that no dynamics can achieve correct convergence in an expected number of steps that is sub-quadratic in $n$, even under a strong version of the model in which activated agents have complete access to the current configuration of the entire system, i.e., the case $\ell=n$. Conversely, we prove that the simple voter model (in which $\ell=1$) correctly solves the problem, while almost matching the aforementioned lower bound. These results suggest that, in contrast to symmetric consensus problems (that do not involve a notion of correct opinion), fast convergence on the correct opinion using stochastic opinion dynamics may indeed require the use of memory. This insight may reflect on natural information dissemination processes that rely on a few knowledgeable individuals.

Stochastic Alignment Processes

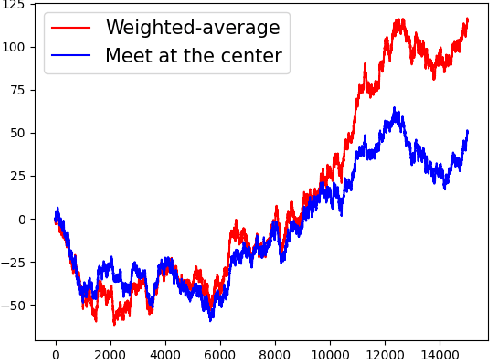
The tendency to align to others is inherent to social behavior, including in animal groups, and flocking in particular. Here we introduce the Stochastic Alignment Problem, aiming to study basic algorithmic aspects that govern alignment processes in unreliable stochastic environments. Consider n birds that aim to maintain a cohesive direction of flight. In each round, each bird receives a noisy measurement of the average direction of others in the group, and consequently updates its orientation. Then, before the next round begins, the orientation is perturbed by random drift (modelling, e.g., the affects of wind). We assume that both noise in measurements and drift follow Gaussian distributions. Upon receiving a measurement, what should be the orientation adjustment policy of birds if their goal is to minimize the average (or maximal) expected deviation of a bird's direction from the average direction? We prove that a distributed weighted-average algorithm, termed W , that at each round balances between the current orientation of a bird and the measurement it receives, maximizes the social welfare. Interestingly, the optimality of this simple distributed algorithm holds even assuming that birds can freely communicate to share their gathered knowledge regarding their past and current measurements. We find this result surprising since it can be shown that birds other than a given i can collectively gather information that is relevant to bird i, yet not processed by it when running a weighted-average algorithm. Intuitively, it seems that optimality is nevertheless achieved, since, when running W , the birds other than i somehow manage to collectively process the aforementioned information in a way that benefits bird i, by turning the average direction towards it. Finally, we also consider the game-theoretic framework, proving that W is the only weighted-average algorithm that is at Nash equilibrium.