Roberto Pereira Silveira
L2M: Practical posterior Laplace approximation with optimization-driven second moment estimation
Jul 09, 2021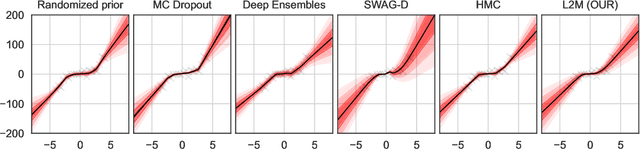
Abstract:Uncertainty quantification for deep neural networks has recently evolved through many techniques. In this work, we revisit Laplace approximation, a classical approach for posterior approximation that is computationally attractive. However, instead of computing the curvature matrix, we show that, under some regularity conditions, the Laplace approximation can be easily constructed using the gradient second moment. This quantity is already estimated by many exponential moving average variants of Adagrad such as Adam and RMSprop, but is traditionally discarded after training. We show that our method (L2M) does not require changes in models or optimization, can be implemented in a few lines of code to yield reasonable results, and it does not require any extra computational steps besides what is already being computed by optimizers, without introducing any new hyperparameter. We hope our method can open new research directions on using quantities already computed by optimizers for uncertainty estimation in deep neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge