Video-based Pedestrian and Vehicle Traffic Analysis During Football Games

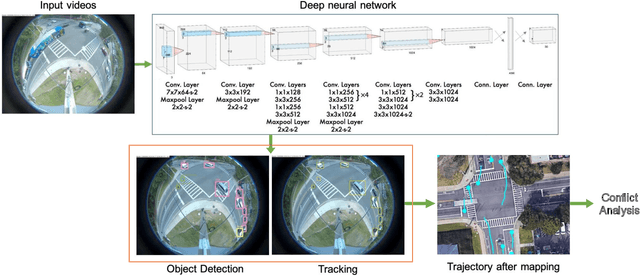
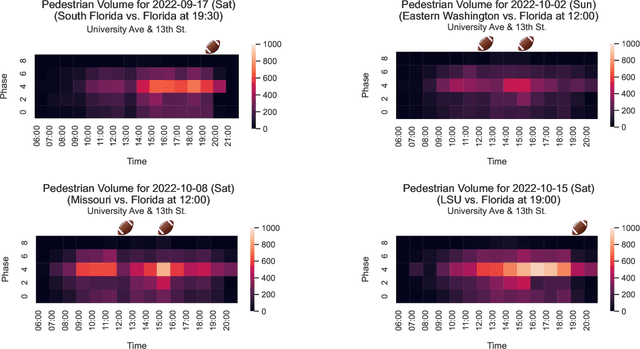
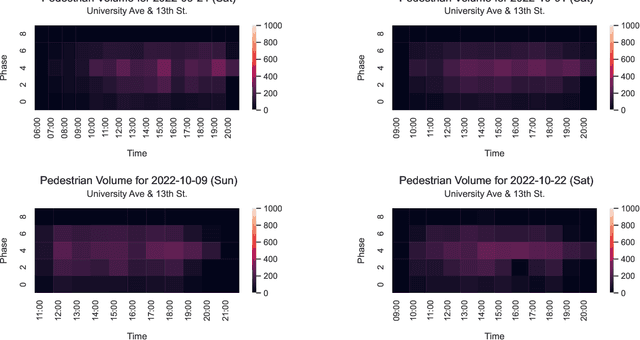
This paper utilizes video analytics to study pedestrian and vehicle traffic behavior, focusing on analyzing traffic patterns during football gamedays. The University of Florida (UF) hosts six to seven home football games on Saturdays during the college football season, attracting significant pedestrian activity. Through video analytics, this study provides valuable insights into the impact of these events on traffic volumes and safety at intersections. Comparing pedestrian and vehicle activities on gamedays versus non-gamedays reveals differing patterns. For example, pedestrian volume substantially increases during gamedays, which is positively correlated with the probability of the away team winning. This correlation is likely because fans of the home team enjoy watching difficult games. Win probabilities as an early predictor of pedestrian volumes at intersections can be a tool to help traffic professionals anticipate traffic management needs. Pedestrian-to-vehicle (P2V) conflicts notably increase on gamedays, particularly a few hours before games start. Addressing this, a "Barnes Dance" movement phase within the intersection is recommended. Law enforcement presence during high-activity gamedays can help ensure pedestrian compliance and enhance safety. In contrast, we identified that vehicle-to-vehicle (V2V) conflicts generally do not increase on gamedays and may even decrease due to heightened driver caution.

Combinatory Adjoints and Differentiation

We develop a compositional approach for automatic and symbolic differentiation based on categorical constructions in functional analysis where derivatives are linear functions on abstract vectors rather than being limited to scalars, vectors, matrices or tensors represented as multi-dimensional arrays. We show that both symbolic and automatic differentiation can be performed using a differential calculus for generating linear functions representing Fr\'echet derivatives based on rules for primitive, constant, linear and bilinear functions as well as their sequential and parallel composition. Linear functions are represented in a combinatory domain-specific language. Finally, we provide a calculus for symbolically computing the adjoint of a derivative without using matrices, which are too inefficient to use on high-dimensional spaces. The resulting symbolic representation of a derivative retains the data-parallel operations from the input program. The combination of combinatory differentiation and computing formal adjoints turns out to be behaviorally equivalent to reverse-mode automatic differentiation. In particular, it provides opportunities for optimizations where matrices are too inefficient to represent linear functions.