Robert Herscovici
Dynamic Batch Adaptation
Aug 01, 2022

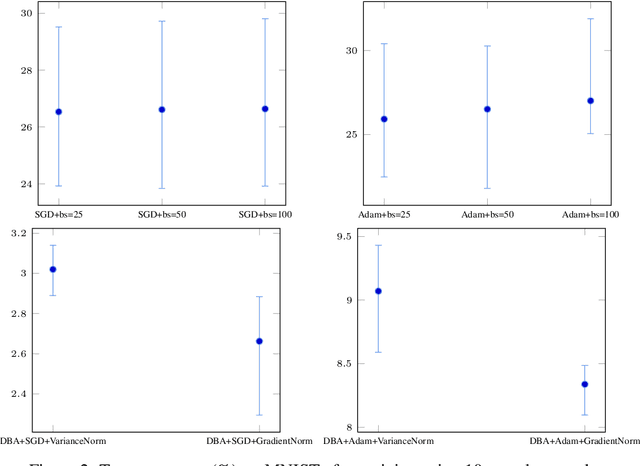

Abstract:Current deep learning adaptive optimizer methods adjust the step magnitude of parameter updates by altering the effective learning rate used by each parameter. Motivated by the known inverse relation between batch size and learning rate on update step magnitudes, we introduce a novel training procedure that dynamically decides the dimension and the composition of the current update step. Our procedure, Dynamic Batch Adaptation (DBA) analyzes the gradients of every sample and selects the subset that best improves certain metrics such as gradient variance for each layer of the network. We present results showing DBA significantly improves the speed of model convergence. Additionally, we find that DBA produces an increased improvement over standard optimizers when used in data scarce conditions where, in addition to convergence speed, it also significantly improves model generalization, managing to train a network with a single fully connected hidden layer using only 1% of the MNIST dataset to reach 97.79% test accuracy. In an even more extreme scenario, it manages to reach 97.44% test accuracy using only 10 samples per class. These results represent a relative error rate reduction of 81.78% and 88.07% respectively, compared to the standard optimizers, Stochastic Gradient Descent (SGD) and Adam.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge