Cristian Simionescu
Deep Learning Training Procedure Augmentations
Nov 25, 2022Abstract:Recent advances in Deep Learning have greatly improved performance on various tasks such as object detection, image segmentation, sentiment analysis. The focus of most research directions up until very recently has been on beating state-of-the-art results. This has materialized in the utilization of bigger and bigger models and techniques which help the training procedure to extract more predictive power out of a given dataset. While this has lead to great results, many of which with real-world applications, other relevant aspects of deep learning have remained neglected and unknown. In this work, we will present several novel deep learning training techniques which, while capable of offering significant performance gains they also reveal several interesting analysis results regarding convergence speed, optimization landscape smoothness, and adversarial robustness. The methods presented in this work are the following: $\bullet$ Perfect Ordering Approximation; a generalized model agnostic curriculum learning approach. The results show the effectiveness of the technique for improving training time as well as offer some new insight into the training process of deep networks. $\bullet$ Cascading Sum Augmentation; an extension of mixup capable of utilizing more data points for linear interpolation by leveraging a smoother optimization landscape. This can be used for computer vision tasks in order to improve both prediction performance as well as improve passive model robustness.
Dynamic Batch Adaptation
Aug 01, 2022

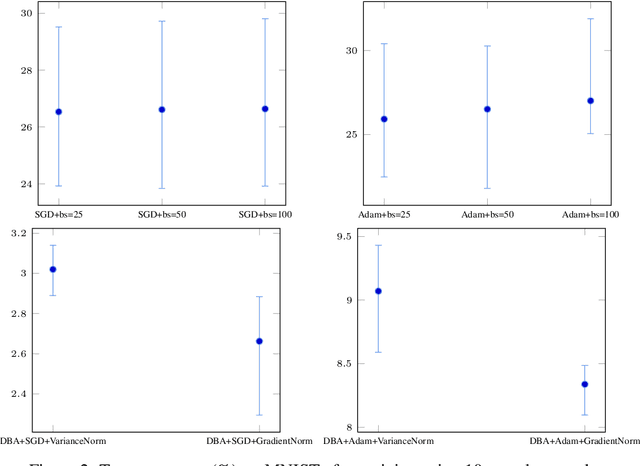

Abstract:Current deep learning adaptive optimizer methods adjust the step magnitude of parameter updates by altering the effective learning rate used by each parameter. Motivated by the known inverse relation between batch size and learning rate on update step magnitudes, we introduce a novel training procedure that dynamically decides the dimension and the composition of the current update step. Our procedure, Dynamic Batch Adaptation (DBA) analyzes the gradients of every sample and selects the subset that best improves certain metrics such as gradient variance for each layer of the network. We present results showing DBA significantly improves the speed of model convergence. Additionally, we find that DBA produces an increased improvement over standard optimizers when used in data scarce conditions where, in addition to convergence speed, it also significantly improves model generalization, managing to train a network with a single fully connected hidden layer using only 1% of the MNIST dataset to reach 97.79% test accuracy. In an even more extreme scenario, it manages to reach 97.44% test accuracy using only 10 samples per class. These results represent a relative error rate reduction of 81.78% and 88.07% respectively, compared to the standard optimizers, Stochastic Gradient Descent (SGD) and Adam.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge