Robert D. Kleinberg
Online Convex Optimization with Unbounded Memory
Oct 18, 2022
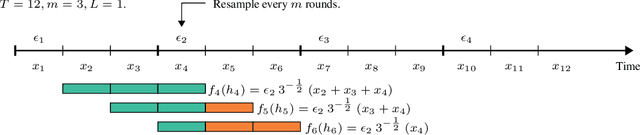
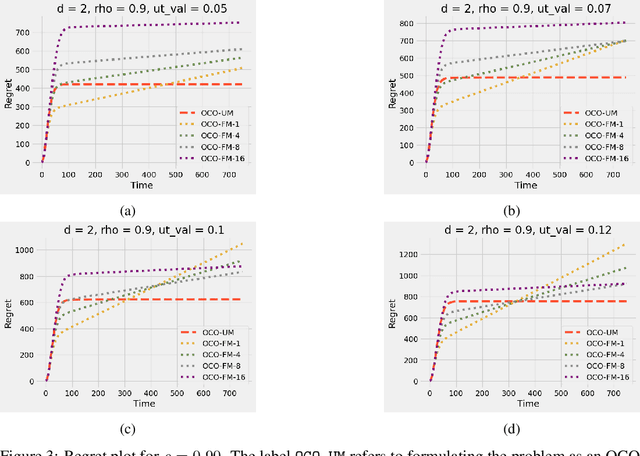
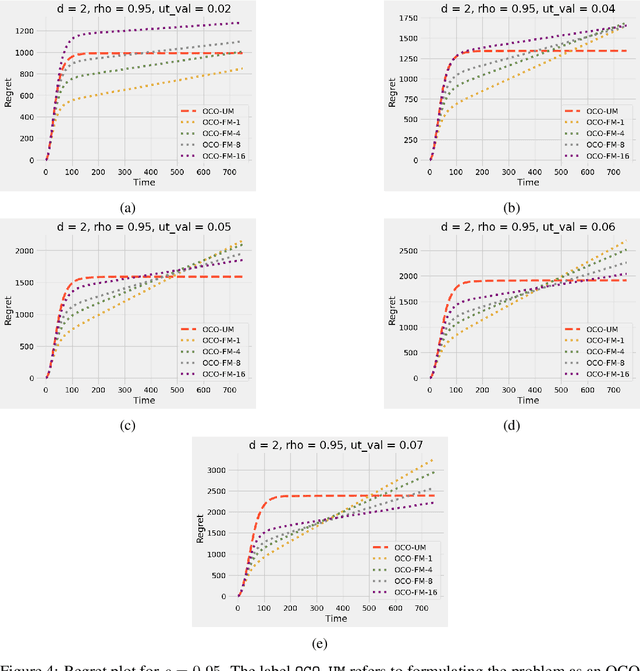
Abstract:Online convex optimization (OCO) is a widely used framework in online learning. In each round, the learner chooses a decision in some convex set and an adversary chooses a convex loss function, and then the learner suffers the loss associated with their chosen decision. However, in many of the motivating applications the loss of the learner depends not only on the current decision but on the entire history of decisions until that point. The OCO framework and existing generalizations thereof fail to capture this. In this work we introduce a generalization of the OCO framework, ``Online Convex Optimization with Unbounded Memory'', that captures long-term dependence on past decisions. We introduce the notion of $p$-effective memory capacity, $H_p$, that quantifies the maximum influence of past decisions on current losses. We prove a $O(\sqrt{H_1 T})$ policy regret bound and a stronger $O(\sqrt{H_p T})$ policy regret bound under mild additional assumptions. These bounds are optimal in terms of their dependence on the time horizon $T$. We show the broad applicability of our framework by using it to derive regret bounds, and to simplify existing regret bound derivations, for a variety of online learning problems including an online variant of performative prediction and online linear control.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge