Convolutional Maximum Mean Discrepancy for Inference in Noisy Data

Modern data analyses frequently encounter settings where samples of variables are contaminated by measurement error. Ignoring measurement noise can substantially degrade statistical inference, while existing correction techniques are often computationally costly and inefficient. Recent advances in kernel methods, particularly those based on Maximum Mean Discrepancy (MMD), have enabled flexible, distribution-free inference, yet typically assume precise data and overlook contamination by measurement error. In this work, we introduce a novel framework for inference with samples corrupted by potentially heteroscedastic noise from a known distribution. Central to our approach is the convolutional MMD (convMMD), which compares distributions after noise convolution and retains metric validity under standard kernel conditions. We establish finite-sample deviation bounds that are unaffected by measurement error and prove an equivalence between testing under noise and kernel smoothing. Leveraging these insights, we introduce a convMMD-based estimator for inference with noisy, heteroscedastic observations. We establish its consistency and asymptotic normality, and provide an efficient implementation using stochastic gradient descent. We demonstrate the practical effectiveness of our approach through simulations and applications in astronomy and social sciences.

I-trustworthy Models. A framework for trustworthiness evaluation of probabilistic classifiers

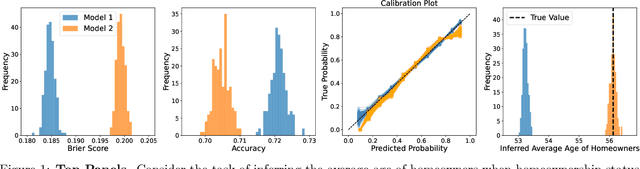
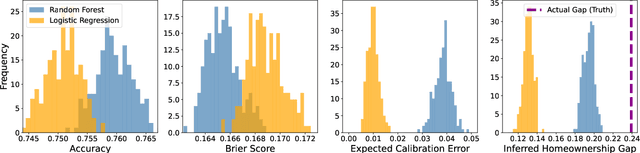
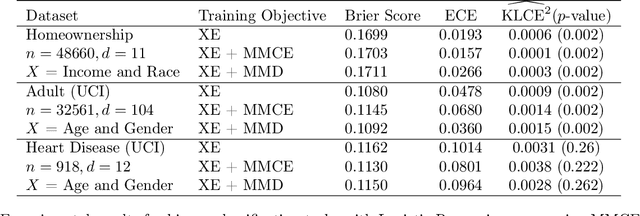
As probabilistic models continue to permeate various facets of our society and contribute to scientific advancements, it becomes a necessity to go beyond traditional metrics such as predictive accuracy and error rates and assess their trustworthiness. Grounded in the competence-based theory of trust, this work formalizes I-trustworthy framework -- a novel framework for assessing the trustworthiness of probabilistic classifiers for inference tasks by linking local calibration to trustworthiness. To assess I-trustworthiness, we use the local calibration error (LCE) and develop a method of hypothesis-testing. This method utilizes a kernel-based test statistic, Kernel Local Calibration Error (KLCE), to test local calibration of a probabilistic classifier. This study provides theoretical guarantees by offering convergence bounds for an unbiased estimator of KLCE. Additionally, we present a diagnostic tool designed to identify and measure biases in cases of miscalibration. The effectiveness of the proposed test statistic is demonstrated through its application to both simulated and real-world datasets. Finally, LCE of related recalibration methods is studied, and we provide evidence of insufficiency of existing methods to achieve I-trustworthiness.

U-Trustworthy Models.Reliability, Competence, and Confidence in Decision-Making

With growing concerns regarding bias and discrimination in predictive models, the AI community has increasingly focused on assessing AI system trustworthiness. Conventionally, trustworthy AI literature relies on the probabilistic framework and calibration as prerequisites for trustworthiness. In this work, we depart from this viewpoint by proposing a novel trust framework inspired by the philosophy literature on trust. We present a precise mathematical definition of trustworthiness, termed $\mathcal{U}$-trustworthiness, specifically tailored for a subset of tasks aimed at maximizing a utility function. We argue that a model's $\mathcal{U}$-trustworthiness is contingent upon its ability to maximize Bayes utility within this task subset. Our first set of results challenges the probabilistic framework by demonstrating its potential to favor less trustworthy models and introduce the risk of misleading trustworthiness assessments. Within the context of $\mathcal{U}$-trustworthiness, we prove that properly-ranked models are inherently $\mathcal{U}$-trustworthy. Furthermore, we advocate for the adoption of the AUC metric as the preferred measure of trustworthiness. By offering both theoretical guarantees and experimental validation, AUC enables robust evaluation of trustworthiness, thereby enhancing model selection and hyperparameter tuning to yield more trustworthy outcomes.