Optimality of Approximate Message Passing Algorithms for Spiked Matrix Models with Rotationally Invariant Noise

We study the problem of estimating a rank one signal matrix from an observed matrix generated by corrupting the signal with additive rotationally invariant noise. We develop a new class of approximate message-passing algorithms for this problem and provide a simple and concise characterization of their dynamics in the high-dimensional limit. At each iteration, these algorithms exploit prior knowledge about the noise structure by applying a non-linear matrix denoiser to the eigenvalues of the observed matrix and prior information regarding the signal structure by applying a non-linear iterate denoiser to the previous iterates generated by the algorithm. We exploit our result on the dynamics of these algorithms to derive the optimal choices for the matrix and iterate denoisers. We show that the resulting algorithm achieves the smallest possible asymptotic estimation error among a broad class of iterative algorithms under a fixed iteration budget.

Statistical-Computational Trade-offs in Tensor PCA and Related Problems via Communication Complexity

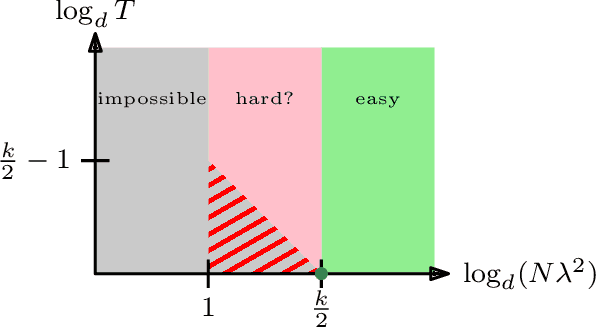
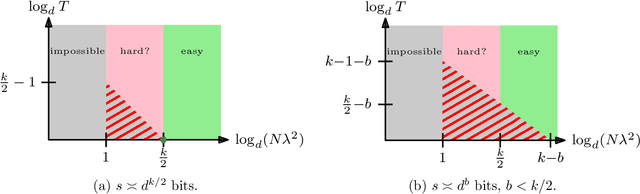
Tensor PCA is a stylized statistical inference problem introduced by Montanari and Richard to study the computational difficulty of estimating an unknown parameter from higher-order moment tensors. Unlike its matrix counterpart, Tensor PCA exhibits a statistical-computational gap, i.e., a sample size regime where the problem is information-theoretically solvable but conjectured to be computationally hard. This paper derives computational lower bounds on the run-time of memory bounded algorithms for Tensor PCA using communication complexity. These lower bounds specify a trade-off among the number of passes through the data sample, the sample size, and the memory required by any algorithm that successfully solves Tensor PCA. While the lower bounds do not rule out polynomial-time algorithms, they do imply that many commonly-used algorithms, such as gradient descent and power method, must have a higher iteration count when the sample size is not large enough. Similar lower bounds are obtained for Non-Gaussian Component Analysis, a family of statistical estimation problems in which low-order moment tensors carry no information about the unknown parameter. Finally, stronger lower bounds are obtained for an asymmetric variant of Tensor PCA and related statistical estimation problems. These results explain why many estimators for these problems use a memory state that is significantly larger than the effective dimensionality of the parameter of interest.

Statistical Query Lower Bounds for Tensor PCA

In the Tensor PCA problem introduced by Richard and Montanari (2014), one is given a dataset consisting of $n$ samples $\mathbf{T}_{1:n}$ of i.i.d. Gaussian tensors of order $k$ with the promise that $\mathbb{E}\mathbf{T}_1$ is a rank-1 tensor and $\|\mathbb{E} \mathbf{T}_1\| = 1$. The goal is to estimate $\mathbb{E} \mathbf{T}_1$. This problem exhibits a large conjectured hard phase when $k>2$: When $d \lesssim n \ll d^{\frac{k}{2}}$ it is information theoretically possible to estimate $\mathbb{E} \mathbf{T}_1$, but no polynomial time estimator is known. We provide a sharp analysis of the optimal sample complexity in the Statistical Query (SQ) model and show that SQ algorithms with polynomial query complexity not only fail to solve Tensor PCA in the conjectured hard phase, but also have a strictly sub-optimal sample complexity compared to some polynomial time estimators such as the Richard-Montanari spectral estimator. Our analysis reveals that the optimal sample complexity in the SQ model depends on whether $\mathbb{E} \mathbf{T}_1$ is symmetric or not. For symmetric, even order tensors, we also isolate a sample size regime in which it is possible to test if $\mathbb{E} \mathbf{T}_1 = \mathbf{0}$ or $\mathbb{E}\mathbf{T}_1 \neq \mathbf{0}$ with polynomially many queries but not estimate $\mathbb{E}\mathbf{T}_1$. Our proofs rely on the Fourier analytic approach of Feldman, Perkins and Vempala (2018) to prove sharp SQ lower bounds.