nSimplex Zen: A Novel Dimensionality Reduction for Euclidean and Hilbert Spaces

Dimensionality reduction techniques map values from a high dimensional space to one with a lower dimension. The result is a space which requires less physical memory and has a faster distance calculation. These techniques are widely used where required properties of the reduced-dimension space give an acceptable accuracy with respect to the original space. Many such transforms have been described. They have been classified in two main groups: linear and topological. Linear methods such as Principal Component Analysis (PCA) and Random Projection (RP) define matrix-based transforms into a lower dimension of Euclidean space. Topological methods such as Multidimensional Scaling (MDS) attempt to preserve higher-level aspects such as the nearest-neighbour relation, and some may be applied to non-Euclidean spaces. Here, we introduce nSimplex Zen, a novel topological method of reducing dimensionality. Like MDS, it relies only upon pairwise distances measured in the original space. The use of distances, rather than coordinates, allows the technique to be applied to both Euclidean and other Hilbert spaces, including those governed by Cosine, Jensen-Shannon and Quadratic Form distances. We show that in almost all cases, due to geometric properties of high-dimensional spaces, our new technique gives better properties than others, especially with reduction to very low dimensions.

A Ptolemaic Partitioning Mechanism

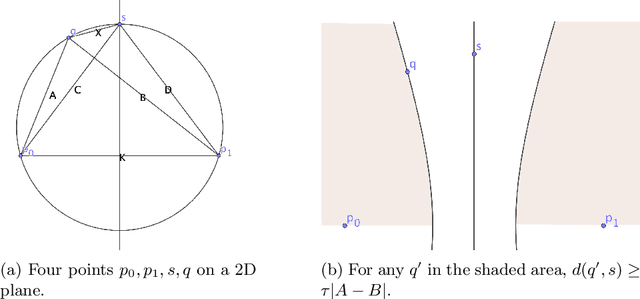
For many years, exact metric search relied upon the property of triangle inequality to give a lower bound on uncalculated distances. Two exclusion mechanisms derive from this property, generally known as pivot exclusion and hyperplane exclusion. These mechanisms work in any proper metric space and are the basis of many metric indexing mechanisms. More recently, the Ptolemaic and four-point lower bound properties have been shown to give tighter bounds in some subclasses of metric space. Both triangle inequality and the four-point lower bound directly imply straightforward partitioning mechanisms: that is, a method of dividing a finite space according to a fixed partition, in order that one or more classes of the partition can be eliminated from a search at query time. However, up to now, no partitioning principle has been identified for the Ptolemaic inequality, which has been used only as a filtering mechanism. Here, a novel partitioning mechanism for the Ptolemaic lower bound is presented. It is always better than either pivot or hyperplane partitioning. While the exclusion condition itself is weaker than Hilbert (four-point) exclusion, its calculation is cheaper. Furthermore, it can be combined with Hilbert exclusion to give a new maximum for exclusion power with respect to the number of distances measured per query.