Rich Sutton
Scalable Online Recurrent Learning Using Columnar Neural Networks
Mar 09, 2021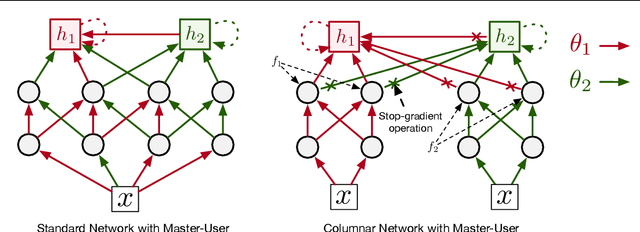
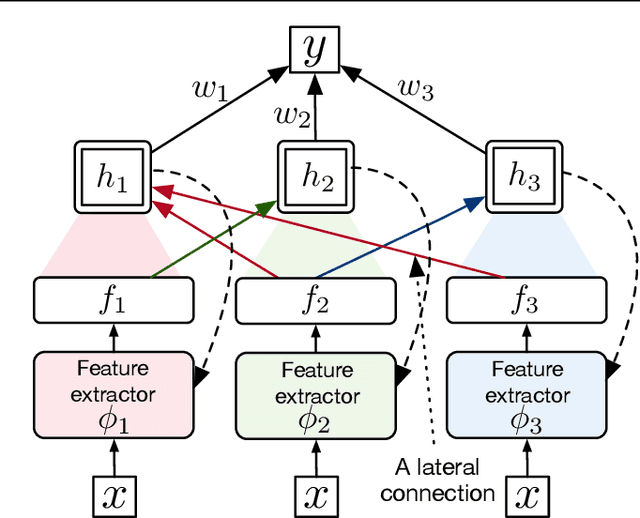
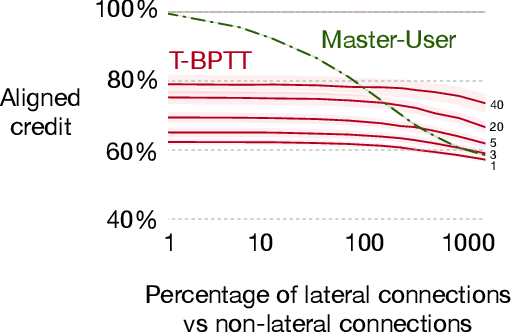
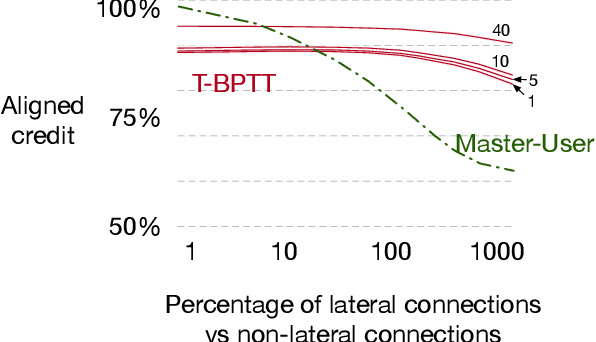
Abstract:Structural credit assignment for recurrent learning is challenging. An algorithm called RTRL can compute gradients for recurrent networks online but is computationally intractable for large networks. Alternatives, such as BPTT, are not online. In this work, we propose a credit-assignment algorithm -- \algoname{} -- that approximates the gradients for recurrent learning in real-time using $O(n)$ operations and memory per-step. Our method builds on the idea that for modular recurrent networks, composed of columns with scalar states, it is sufficient for a parameter to only track its influence on the state of its column. We empirically show that as long as connections between columns are sparse, our method approximates the true gradient well. In the special case when there are no connections between columns, the $O(n)$ gradient estimate is exact. We demonstrate the utility of the approach for both recurrent state learning and meta-learning by comparing the estimated gradient to the true gradient on a synthetic test-bed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge