Robust Representation Learning in Masked Autoencoders

Masked Autoencoders (MAEs) achieve impressive performance in image classification tasks, yet the internal representations they learn remain less understood. This work started as an attempt to understand the strong downstream classification performance of MAE. In this process we discover that representations learned with the pretraining and fine-tuning, are quite robust - demonstrating a good classification performance in the presence of degradations, such as blur and occlusions. Through layer-wise analysis of token embeddings, we show that pretrained MAE progressively constructs its latent space in a class-aware manner across network depth: embeddings from different classes lie in subspaces that become increasingly separable. We further observe that MAE exhibits early and persistent global attention across encoder layers, in contrast to standard Vision Transformers (ViTs). To quantify feature robustness, we introduce two sensitivity indicators: directional alignment between clean and perturbed embeddings, and head-wise retention of active features under degradations. These studies help establish the robust classification performance of MAEs.

Latent Space Characterization of Autoencoder Variants

Understanding the latent spaces learned by deep learning models is crucial in exploring how they represent and generate complex data. Autoencoders (AEs) have played a key role in the area of representation learning, with numerous regularization techniques and training principles developed not only to enhance their ability to learn compact and robust representations, but also to reveal how different architectures influence the structure and smoothness of the lower-dimensional non-linear manifold. We strive to characterize the structure of the latent spaces learned by different autoencoders including convolutional autoencoders (CAEs), denoising autoencoders (DAEs), and variational autoencoders (VAEs) and how they change with the perturbations in the input. By characterizing the matrix manifolds corresponding to the latent spaces, we provide an explanation for the well-known observation that the latent spaces of CAE and DAE form non-smooth manifolds, while that of VAE forms a smooth manifold. We also map the points of the matrix manifold to a Hilbert space using distance preserving transforms and provide an alternate view in terms of the subspaces generated in the Hilbert space as a function of the distortion in the input. The results show that the latent manifolds of CAE and DAE are stratified with each stratum being a smooth product manifold, while the manifold of VAE is a smooth product manifold of two symmetric positive definite matrices and a symmetric positive semi-definite matrix.

Lossless Image Compression Using Multi-level Dictionaries: Binary Images

Lossless image compression is required in various applications to reduce storage or transmission costs of images, while requiring the reconstructed images to have zero information loss compared to the original. Existing lossless image compression methods either have simple design but poor compression performance, or complex design, better performance, but with no performance guarantees. In our endeavor to develop a lossless image compression method with low complexity and guaranteed performance, we argue that compressibility of a color image is essentially derived from the patterns in its spatial structure, intensity variations, and color variations. Thus, we divide the overall design of a lossless image compression scheme into three parts that exploit corresponding redundancies. We further argue that the binarized version of an image captures its fundamental spatial structure and in this work, we propose a scheme for lossless compression of binary images. The proposed scheme first learns dictionaries of $16\times16$, $8\times8$, $4\times4$, and $2\times 2$ square pixel patterns from various datasets of binary images. It then uses these dictionaries to encode binary images. These dictionaries have various interesting properties that are further exploited to construct an efficient scheme. Our preliminary results show that the proposed scheme consistently outperforms existing conventional and learning based lossless compression approaches, and provides, on average, as much as $1.5\times$ better performance than a common general purpose lossless compression scheme (WebP), more than $3\times$ better performance than a state of the art learning based scheme, and better performance than a specialized scheme for binary image compression (JBIG2).

Learning optimally separated class-specific subspace representations using convolutional autoencoder

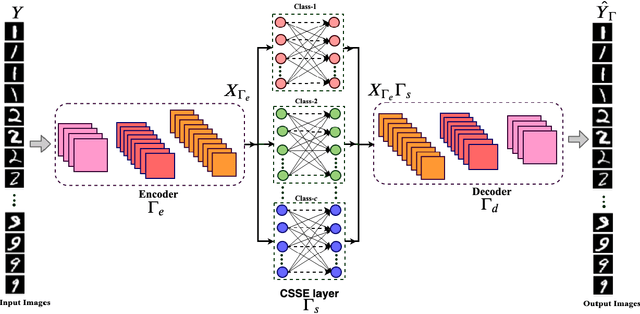
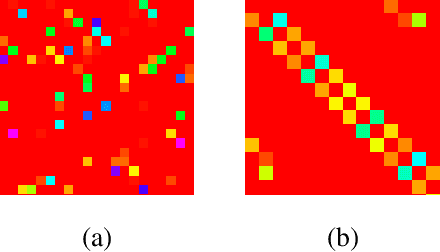
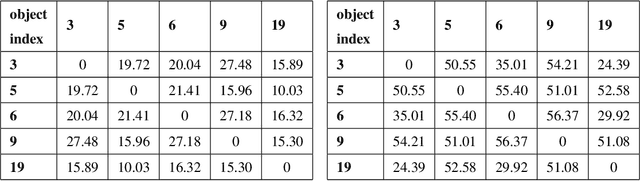
In this work, we propose a novel convolutional autoencoder based architecture to generate subspace specific feature representations that are best suited for classification task. The class-specific data is assumed to lie in low dimensional linear subspaces, which could be noisy and not well separated, i.e., subspace distance (principal angle) between two classes is very low. The proposed network uses a novel class-specific self expressiveness (CSSE) layer sandwiched between encoder and decoder networks to generate class-wise subspace representations which are well separated. The CSSE layer along with encoder/ decoder are trained in such a way that data still lies in subspaces in the feature space with minimum principal angle much higher than that of the input space. To demonstrate the effectiveness of the proposed approach, several experiments have been carried out on state-of-the-art machine learning datasets and a significant improvement in classification performance is observed over existing subspace based transformation learning methods.