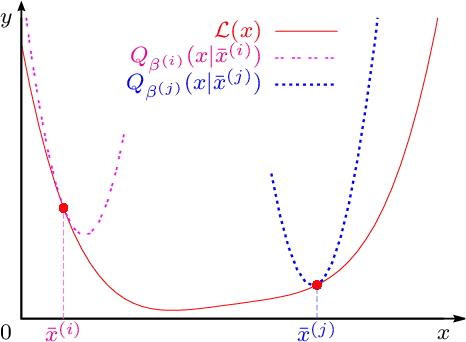
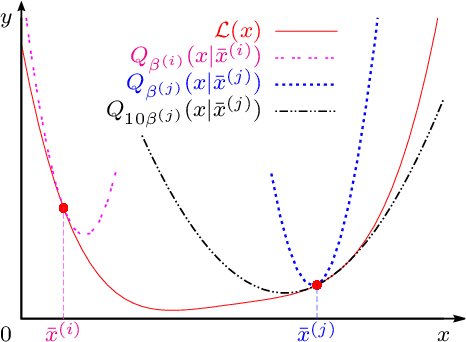
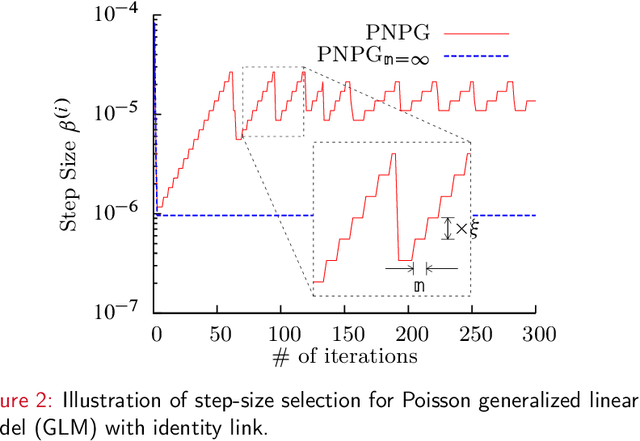
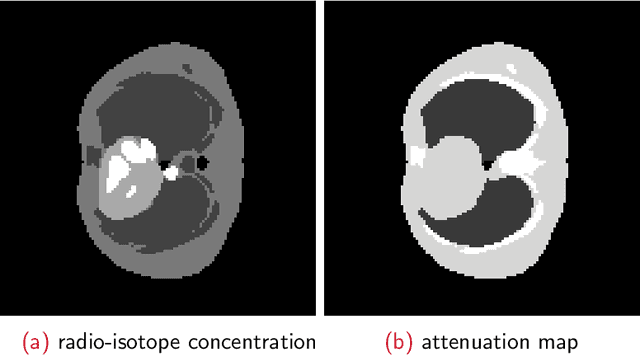
Projected Nesterov's Proximal-Gradient Algorithm for Sparse Signal Reconstruction with a Convex Constraint

We develop a projected Nesterov's proximal-gradient (PNPG) approach for sparse signal reconstruction that combines adaptive step size with Nesterov's momentum acceleration. The objective function that we wish to minimize is the sum of a convex differentiable data-fidelity (negative log-likelihood (NLL)) term and a convex regularization term. We apply sparse signal regularization where the signal belongs to a closed convex set within the closure of the domain of the NLL; the convex-set constraint facilitates flexible NLL domains and accurate signal recovery. Signal sparsity is imposed using the $\ell_1$-norm penalty on the signal's linear transform coefficients or gradient map, respectively. The PNPG approach employs projected Nesterov's acceleration step with restart and an inner iteration to compute the proximal mapping. We propose an adaptive step-size selection scheme to obtain a good local majorizing function of the NLL and reduce the time spent backtracking. Thanks to step-size adaptation, PNPG does not require Lipschitz continuity of the gradient of the NLL. We present an integrated derivation of the momentum acceleration and its $\mathcal{O}(k^{-2})$ convergence-rate and iterate convergence proofs, which account for adaptive step-size selection, inexactness of the iterative proximal mapping, and the convex-set constraint. The tuning of PNPG is largely application-independent. Tomographic and compressed-sensing reconstruction experiments with Poisson generalized linear and Gaussian linear measurement models demonstrate the performance of the proposed approach.

Mask Iterative Hard Thresholding Algorithms for Sparse Image Reconstruction of Objects with Known Contour

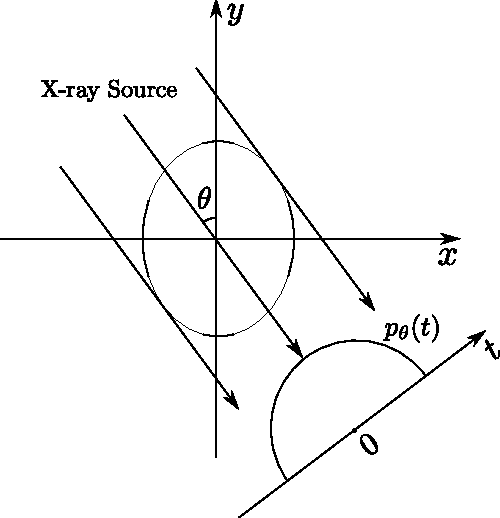
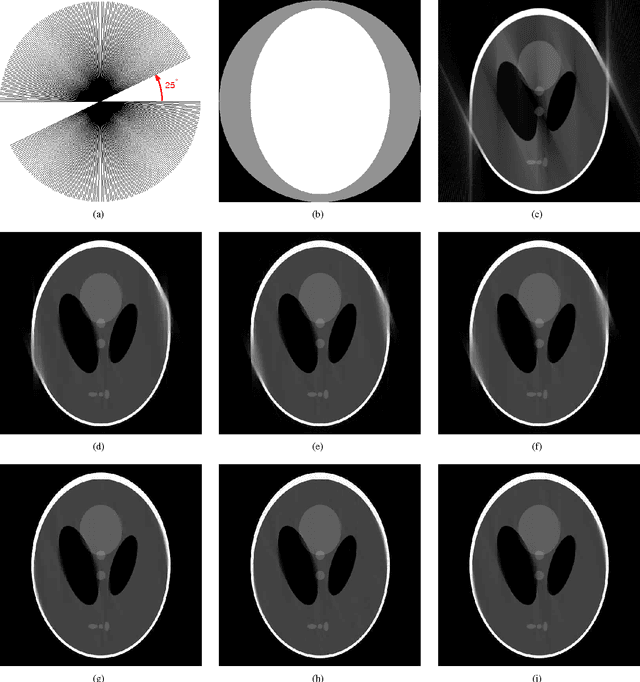
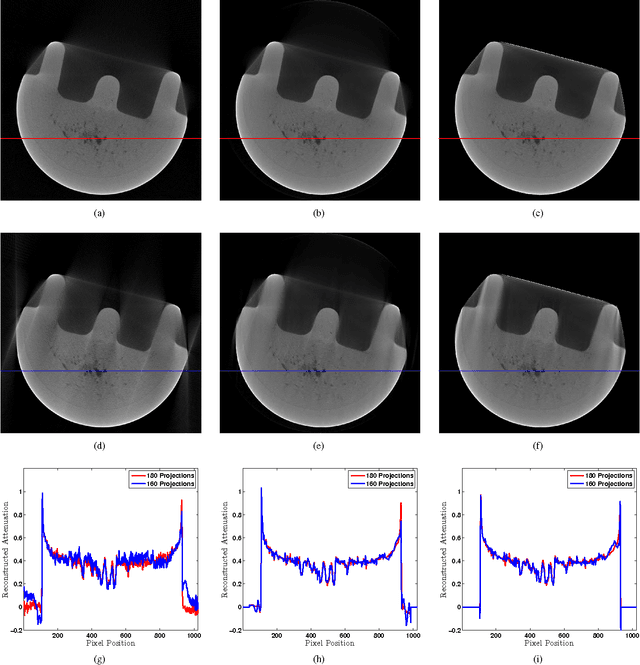
We develop mask iterative hard thresholding algorithms (mask IHT and mask DORE) for sparse image reconstruction of objects with known contour. The measurements follow a noisy underdetermined linear model common in the compressive sampling literature. Assuming that the contour of the object that we wish to reconstruct is known and that the signal outside the contour is zero, we formulate a constrained residual squared error minimization problem that incorporates both the geometric information (i.e. the knowledge of the object's contour) and the signal sparsity constraint. We first introduce a mask IHT method that aims at solving this minimization problem and guarantees monotonically non-increasing residual squared error for a given signal sparsity level. We then propose a double overrelaxation scheme for accelerating the convergence of the mask IHT algorithm. We also apply convex mask reconstruction approaches that employ a convex relaxation of the signal sparsity constraint. In X-ray computed tomography (CT), we propose an automatic scheme for extracting the convex hull of the inspected object from the measured sinograms; the obtained convex hull is used to capture the object contour information. We compare the proposed mask reconstruction schemes with the existing large-scale sparse signal reconstruction methods via numerical simulations and demonstrate that, by exploiting both the geometric contour information of the underlying image and sparsity of its wavelet coefficients, we can reconstruct this image using a significantly smaller number of measurements than the existing methods.