A Max-Product EM Algorithm for Reconstructing Markov-tree Sparse Signals from Compressive Samples

We propose a Bayesian expectation-maximization (EM) algorithm for reconstructing Markov-tree sparse signals via belief propagation. The measurements follow an underdetermined linear model where the regression-coefficient vector is the sum of an unknown approximately sparse signal and a zero-mean white Gaussian noise with an unknown variance. The signal is composed of large- and small-magnitude components identified by binary state variables whose probabilistic dependence structure is described by a Markov tree. Gaussian priors are assigned to the signal coefficients given their state variables and the Jeffreys' noninformative prior is assigned to the noise variance. Our signal reconstruction scheme is based on an EM iteration that aims at maximizing the posterior distribution of the signal and its state variables given the noise variance. We construct the missing data for the EM iteration so that the complete-data posterior distribution corresponds to a hidden Markov tree (HMT) probabilistic graphical model that contains no loops and implement its maximization (M) step via a max-product algorithm. This EM algorithm estimates the vector of state variables as well as solves iteratively a linear system of equations to obtain the corresponding signal estimate. We select the noise variance so that the corresponding estimated signal and state variables obtained upon convergence of the EM iteration have the largest marginal posterior distribution. We compare the proposed and existing state-of-the-art reconstruction methods via signal and image reconstruction experiments.

Mask Iterative Hard Thresholding Algorithms for Sparse Image Reconstruction of Objects with Known Contour

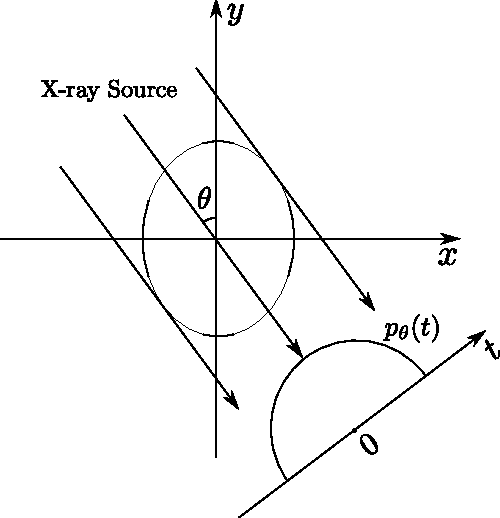
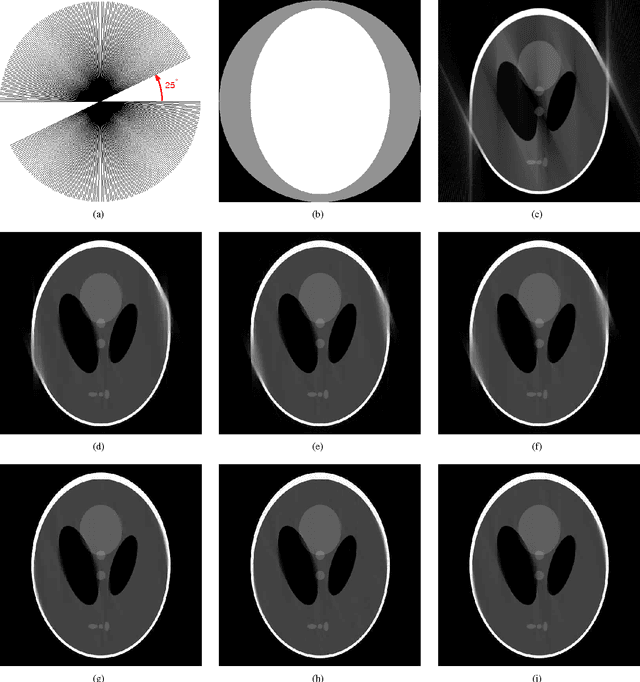
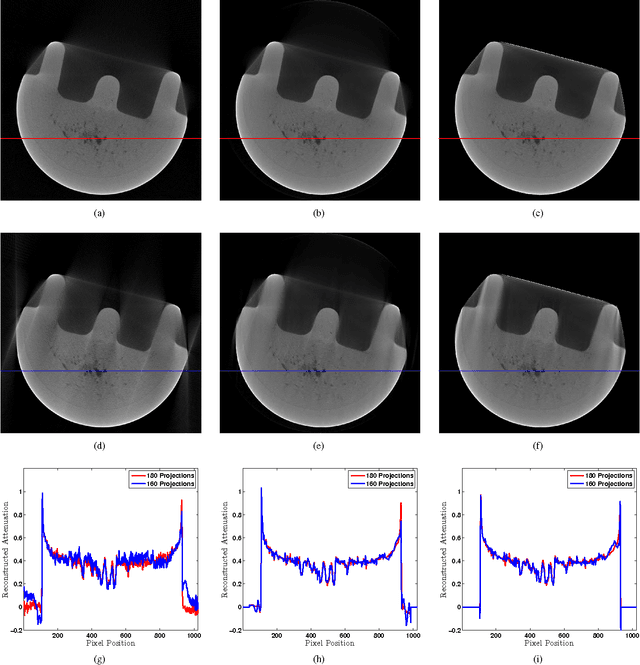
We develop mask iterative hard thresholding algorithms (mask IHT and mask DORE) for sparse image reconstruction of objects with known contour. The measurements follow a noisy underdetermined linear model common in the compressive sampling literature. Assuming that the contour of the object that we wish to reconstruct is known and that the signal outside the contour is zero, we formulate a constrained residual squared error minimization problem that incorporates both the geometric information (i.e. the knowledge of the object's contour) and the signal sparsity constraint. We first introduce a mask IHT method that aims at solving this minimization problem and guarantees monotonically non-increasing residual squared error for a given signal sparsity level. We then propose a double overrelaxation scheme for accelerating the convergence of the mask IHT algorithm. We also apply convex mask reconstruction approaches that employ a convex relaxation of the signal sparsity constraint. In X-ray computed tomography (CT), we propose an automatic scheme for extracting the convex hull of the inspected object from the measured sinograms; the obtained convex hull is used to capture the object contour information. We compare the proposed mask reconstruction schemes with the existing large-scale sparse signal reconstruction methods via numerical simulations and demonstrate that, by exploiting both the geometric contour information of the underlying image and sparsity of its wavelet coefficients, we can reconstruct this image using a significantly smaller number of measurements than the existing methods.