Heuristics, Answer Set Programming and Markov Decision Process for Solving a Set of Spatial Puzzles

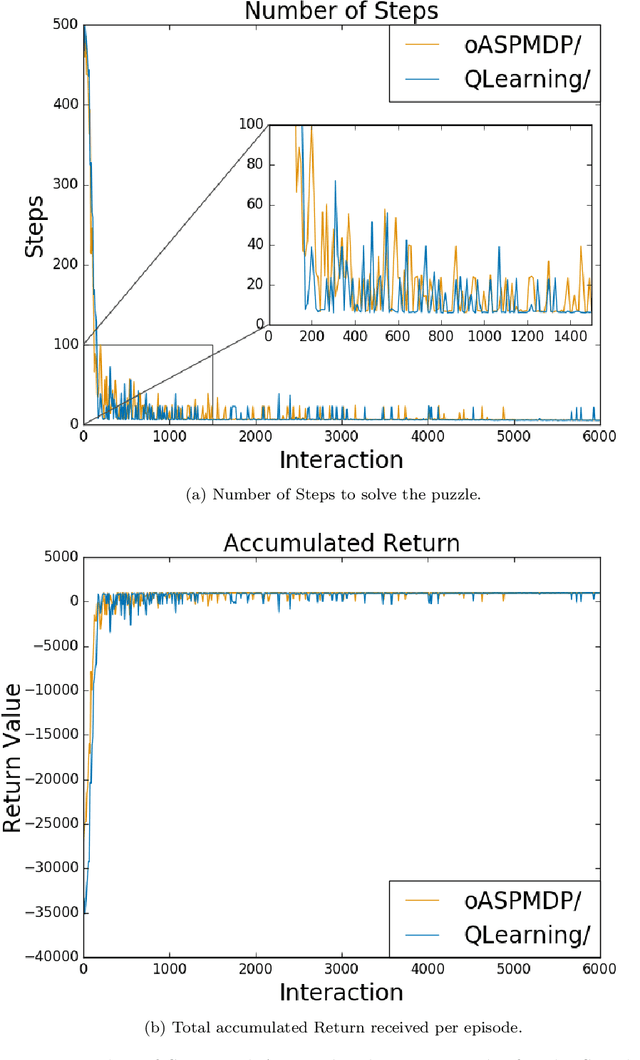
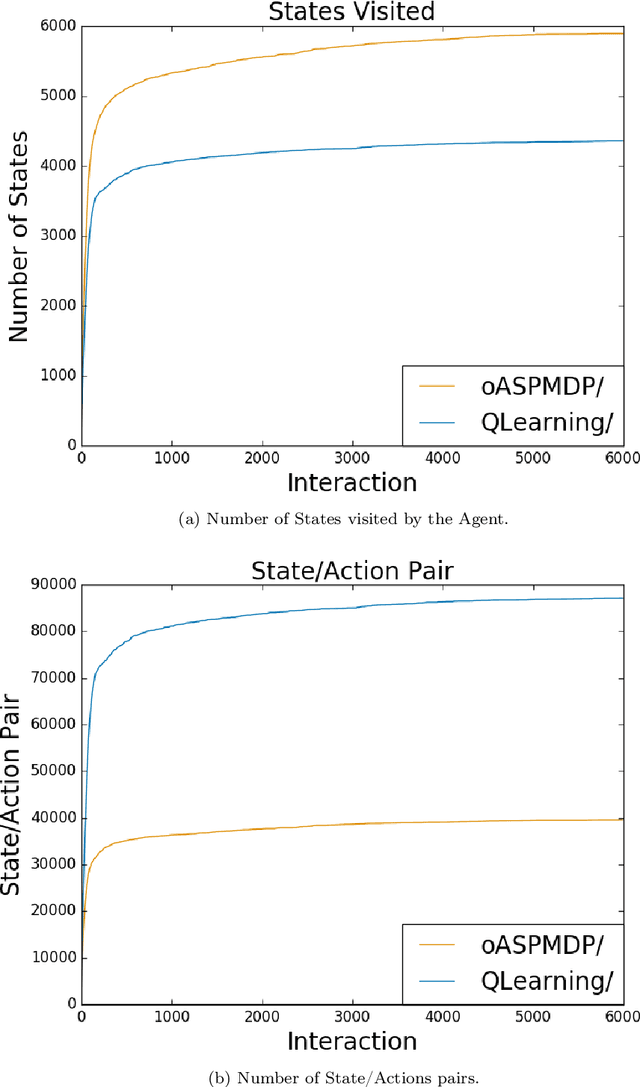
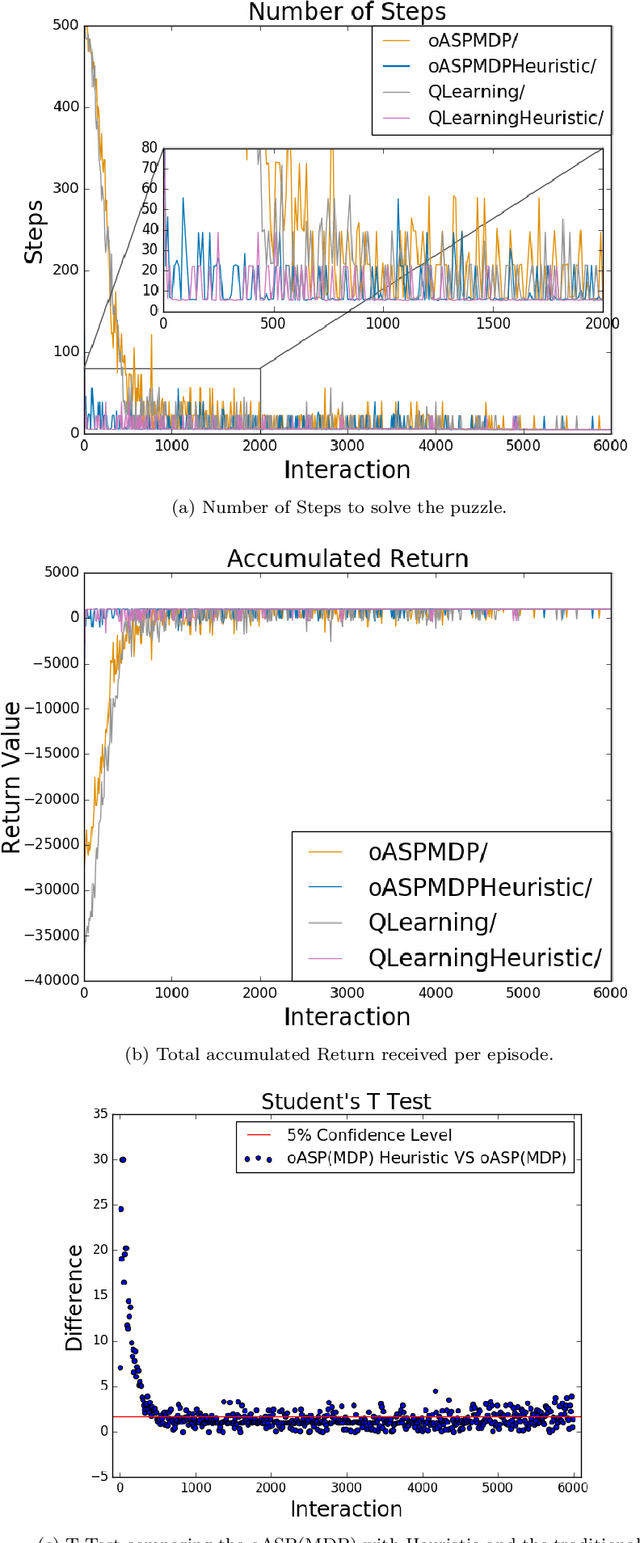
Spatial puzzles composed of rigid objects, flexible strings and holes offer interesting domains for reasoning about spatial entities that are common in the human daily-life's activities. The goal of this work is to investigate the automated solution of this kind of puzzles adapting an algorithm that combines Answer Set Programming (ASP) with Markov Decision Process (MDP), algorithm oASP(MDP), to use heuristics accelerating the learning process. ASP is applied to represent the domain as an MDP, while a Reinforcement Learning algorithm (Q-Learning) is used to find the optimal policies. In this work, the heuristics were obtained from the solution of relaxed versions of the puzzles. Experiments were performed on deterministic, non-deterministic and non-stationary versions of the puzzles. Results show that the proposed approach can accelerate the learning process, presenting an advantage when compared to the non-heuristic versions of oASP(MDP) and Q-Learning.

A method for the online construction of the set of states of a Markov Decision Process using Answer Set Programming

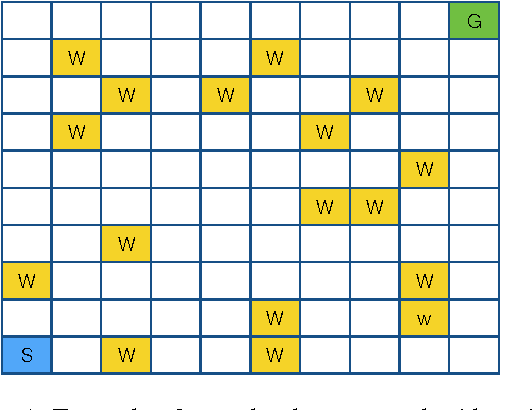
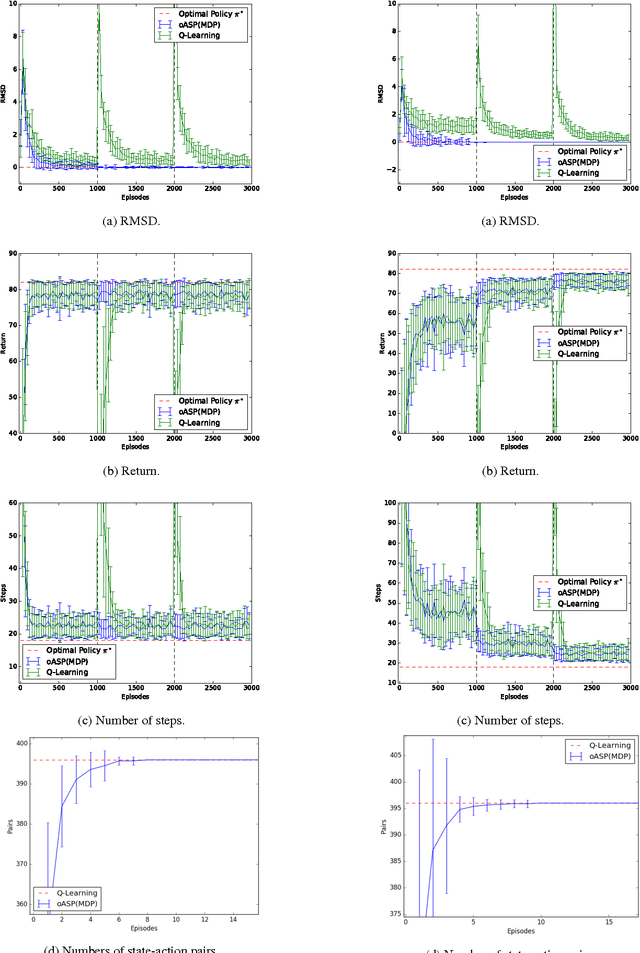
Non-stationary domains, that change in unpredicted ways, are a challenge for agents searching for optimal policies in sequential decision-making problems. This paper presents a combination of Markov Decision Processes (MDP) with Answer Set Programming (ASP), named {\em Online ASP for MDP} (oASP(MDP)), which is a method capable of constructing the set of domain states while the agent interacts with a changing environment. oASP(MDP) updates previously obtained policies, learnt by means of Reinforcement Learning (RL), using rules that represent the domain changes observed by the agent. These rules represent a set of domain constraints that are processed as ASP programs reducing the search space. Results show that oASP(MDP) is capable of finding solutions for problems in non-stationary domains without interfering with the action-value function approximation process.

Answer Set Programming for Non-Stationary Markov Decision Processes

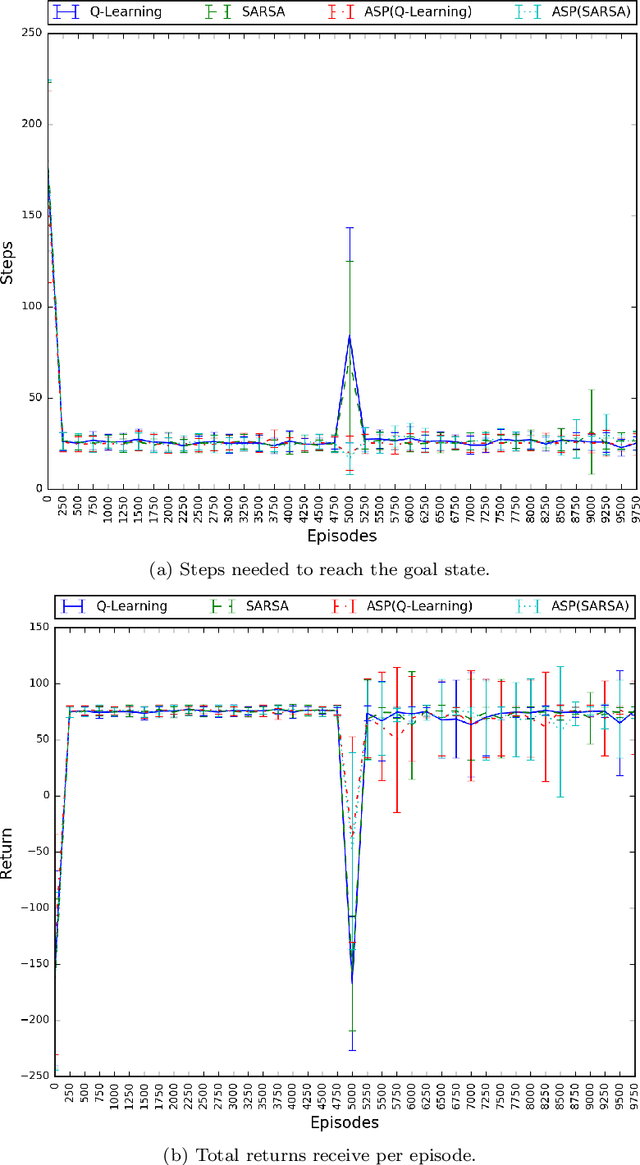
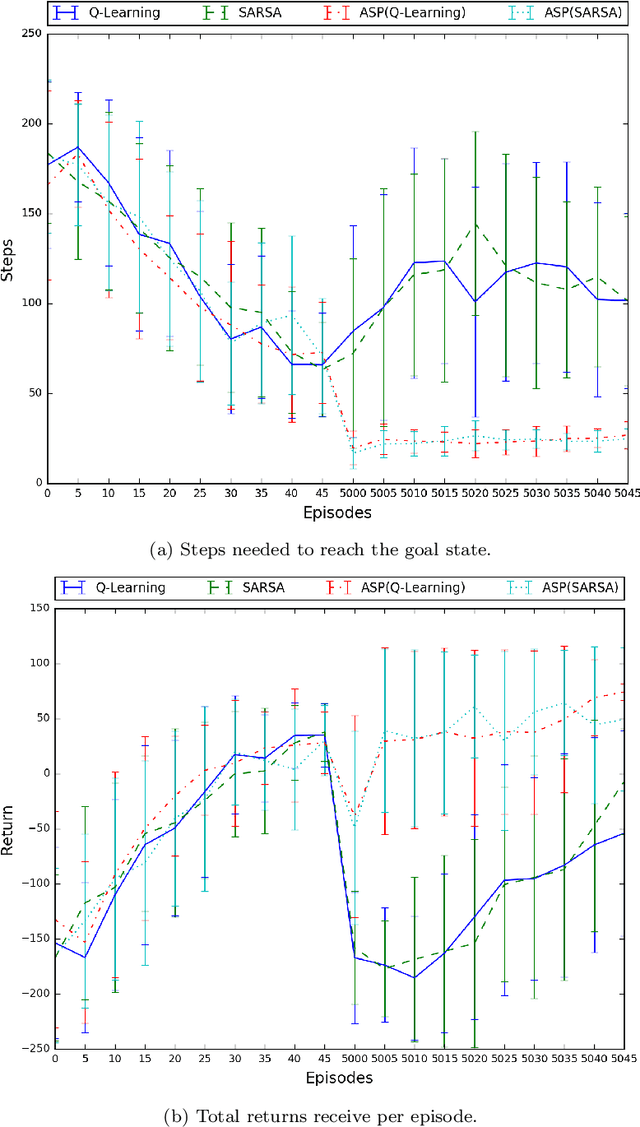
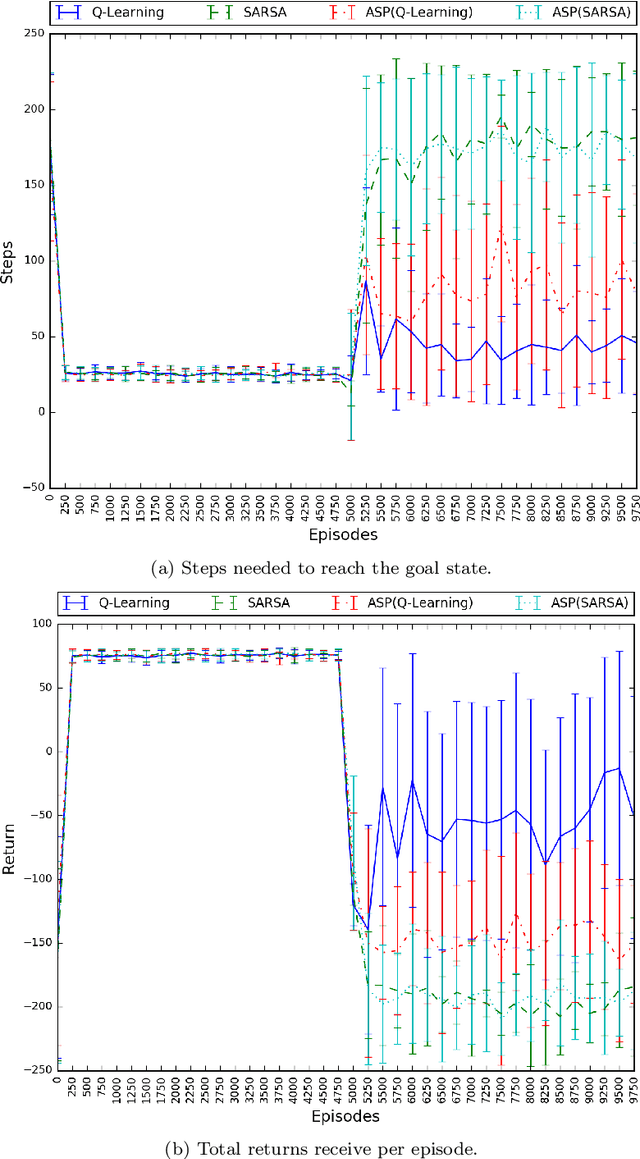
Non-stationary domains, where unforeseen changes happen, present a challenge for agents to find an optimal policy for a sequential decision making problem. This work investigates a solution to this problem that combines Markov Decision Processes (MDP) and Reinforcement Learning (RL) with Answer Set Programming (ASP) in a method we call ASP(RL). In this method, Answer Set Programming is used to find the possible trajectories of an MDP, from where Reinforcement Learning is applied to learn the optimal policy of the problem. Results show that ASP(RL) is capable of efficiently finding the optimal solution of an MDP representing non-stationary domains.