Multi-Flow Transmission in Wireless Interference Networks: A Convergent Graph Learning Approach

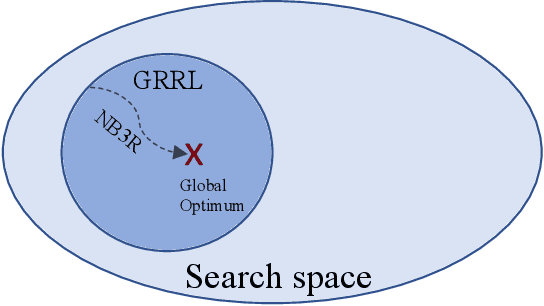
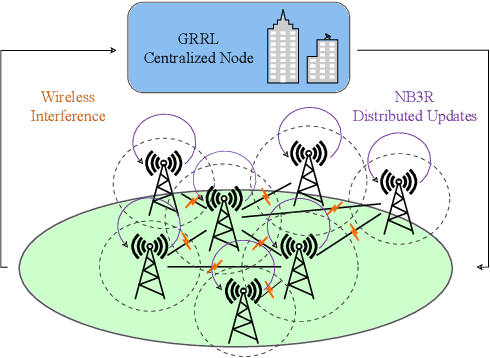
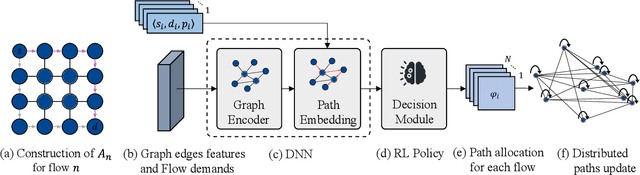
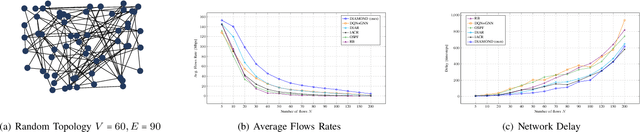
We consider the problem of of multi-flow transmission in wireless networks, where data signals from different flows can interfere with each other due to mutual interference between links along their routes, resulting in reduced link capacities. The objective is to develop a multi-flow transmission strategy that routes flows across the wireless interference network to maximize the network utility. However, obtaining an optimal solution is computationally expensive due to the large state and action spaces involved. To tackle this challenge, we introduce a novel algorithm called Dual-stage Interference-Aware Multi-flow Optimization of Network Data-signals (DIAMOND). The design of DIAMOND allows for a hybrid centralized-distributed implementation, which is a characteristic of 5G and beyond technologies with centralized unit deployments. A centralized stage computes the multi-flow transmission strategy using a novel design of graph neural network (GNN) reinforcement learning (RL) routing agent. Then, a distributed stage improves the performance based on a novel design of distributed learning updates. We provide a theoretical analysis of DIAMOND and prove that it converges to the optimal multi-flow transmission strategy as time increases. We also present extensive simulation results over various network topologies (random deployment, NSFNET, GEANT2), demonstrating the superior performance of DIAMOND compared to existing methods.

Accelerated Gradient Descent Learning over Multiple Access Fading Channels

We consider a distributed learning problem in a wireless network, consisting of N distributed edge devices and a parameter server (PS). The objective function is a sum of the edge devices' local loss functions, who aim to train a shared model by communicating with the PS over multiple access channels (MAC). This problem has attracted a growing interest in distributed sensing systems, and more recently in federated learning, known as over-the-air computation. In this paper, we develop a novel Accelerated Gradient-descent Multiple Access (AGMA) algorithm that uses momentum-based gradient signals over noisy fading MAC to improve the convergence rate as compared to existing methods. Furthermore, AGMA does not require power control or beamforming to cancel the fading effect, which simplifies the implementation complexity. We analyze AGMA theoretically, and establish a finite-sample bound of the error for both convex and strongly convex loss functions with Lipschitz gradient. For the strongly convex case, we show that AGMA approaches the best-known linear convergence rate as the network increases. For the convex case, we show that AGMA significantly improves the sub-linear convergence rate as compared to existing methods. Finally, we present simulation results using real datasets that demonstrate better performance by AGMA.