Low-Rank Boolean Matrix Approximation by Integer Programming

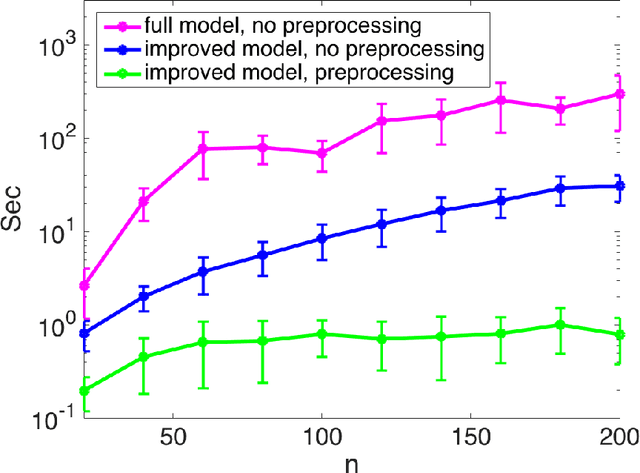
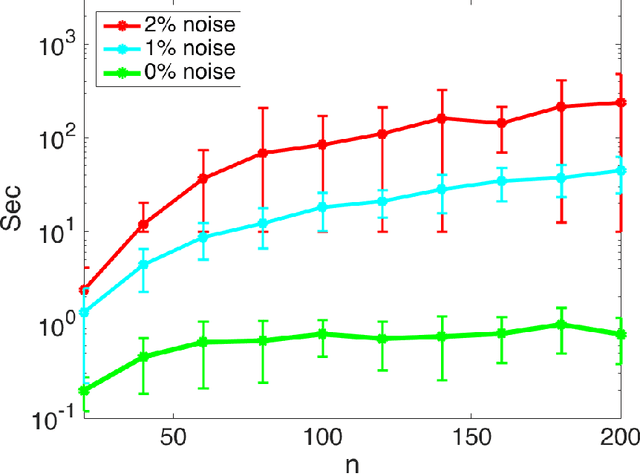
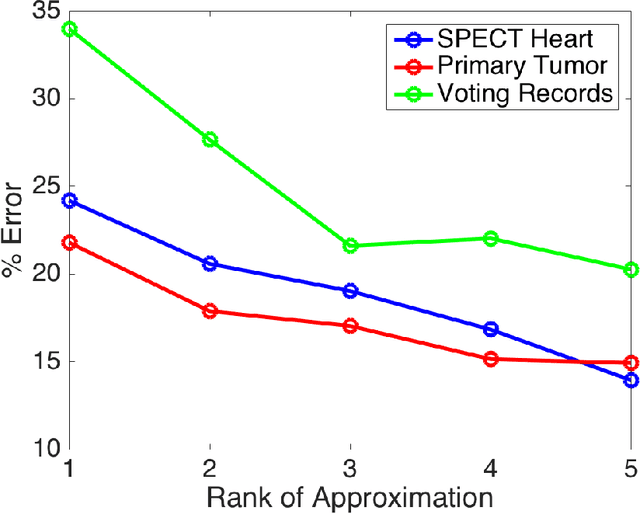
Low-rank approximations of data matrices are an important dimensionality reduction tool in machine learning and regression analysis. We consider the case of categorical variables, where it can be formulated as the problem of finding low-rank approximations to Boolean matrices. In this paper we give what is to the best of our knowledge the first integer programming formulation that relies on only polynomially many variables and constraints, we discuss how to solve it computationally and report numerical tests on synthetic and real-world data.

3D Image Reconstruction from X-Ray Measurements with Overlap

3D image reconstruction from a set of X-ray projections is an important image reconstruction problem, with applications in medical imaging, industrial inspection and airport security. The innovation of X-ray emitter arrays allows for a novel type of X-ray scanners with multiple simultaneously emitting sources. However, two or more sources emitting at the same time can yield measurements from overlapping rays, imposing a new type of image reconstruction problem based on nonlinear constraints. Using traditional linear reconstruction methods, respective scanner geometries have to be implemented such that no rays overlap, which severely restricts the scanner design. We derive a new type of 3D image reconstruction model with nonlinear constraints, based on measurements with overlapping X-rays. Further, we show that the arising optimization problem is partially convex, and present an algorithm to solve it. Experiments show highly improved image reconstruction results from both simulated and real-world measurements.