Ralph Kenna
Temporal Network Analysis of Literary Texts
Feb 22, 2016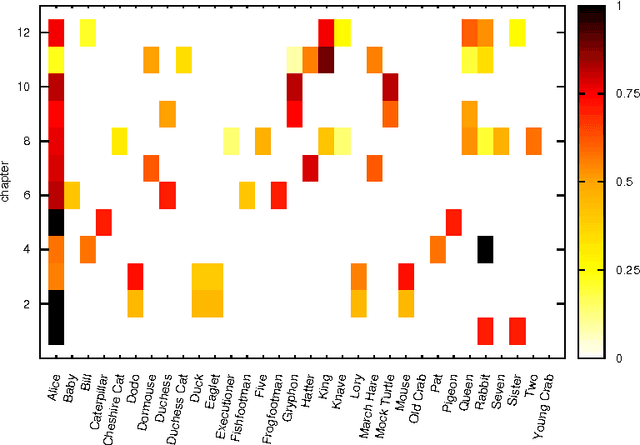
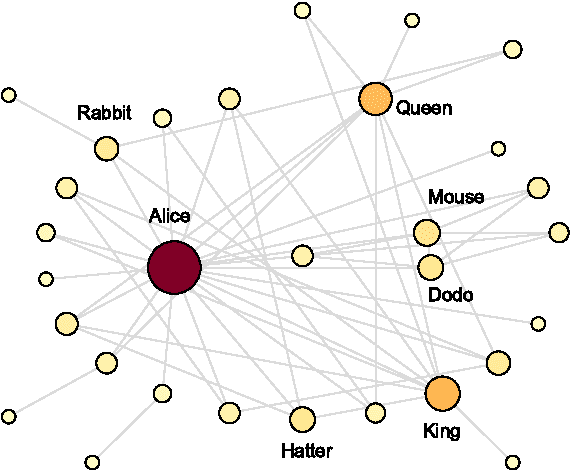
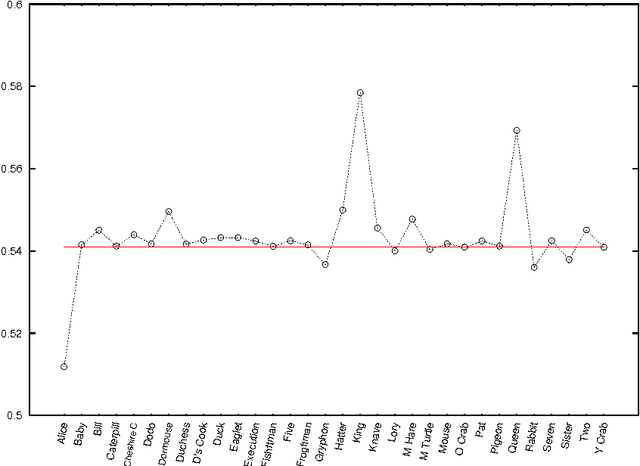
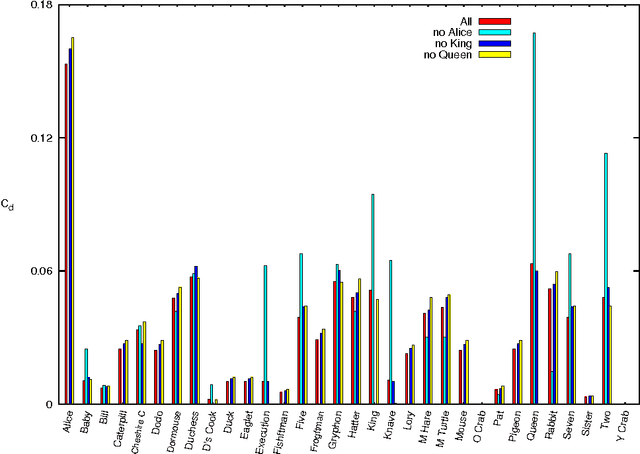
Abstract:We study temporal networks of characters in literature focusing on "Alice's Adventures in Wonderland" (1865) by Lewis Carroll and the anonymous "La Chanson de Roland" (around 1100). The former, one of the most influential pieces of nonsense literature ever written, describes the adventures of Alice in a fantasy world with logic plays interspersed along the narrative. The latter, a song of heroic deeds, depicts the Battle of Roncevaux in 778 A.D. during Charlemagne's campaign on the Iberian Peninsula. We apply methods recently developed by Taylor and coworkers \cite{Taylor+2015} to find time-averaged eigenvector centralities, Freeman indices and vitalities of characters. We show that temporal networks are more appropriate than static ones for studying stories, as they capture features that the time-independent approaches fail to yield.
Universal Properties of Mythological Networks
Jul 18, 2012
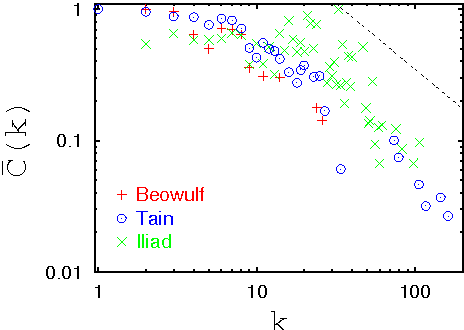
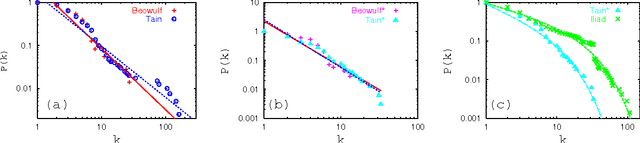

Abstract:As in statistical physics, the concept of universality plays an important, albeit qualitative, role in the field of comparative mythology. Here we apply statistical mechanical tools to analyse the networks underlying three iconic mythological narratives with a view to identifying common and distinguishing quantitative features. Of the three narratives, an Anglo-Saxon and a Greek text are mostly believed by antiquarians to be partly historically based while the third, an Irish epic, is often considered to be fictional. Here we show that network analysis is able to discriminate real from imaginary social networks and place mythological narratives on the spectrum between them. Moreover, the perceived artificiality of the Irish narrative can be traced back to anomalous features associated with six characters. Considering these as amalgams of several entities or proxies, renders the plausibility of the Irish text comparable to the others from a network-theoretic point of view.
* 6 pages, 3 figures, 2 tables. Updated to incorporate corrections from EPL acceptance process
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge